题目内容
(1)已知恒等式x3-x2-x+1=(x-1)(x2+kx-1),求k的值;
(2)若x是整数,求证: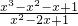 是整数.
是整数.
解:(1)由题设知,(x-1)(x2+kx-1)=x3+(k-1)x2-(k+1)x+1,
所以x3-x2-x+1=x3+(k-1)x2-(k+1)x+1,
从而有k-1=-1,-k-1=-1,
解得k=0.
故所求k的值为0;
(2)由(1)知k=0,则x3-x2-x+1=(x-1)(x2-1)=(x-1)2(x+1),
∴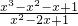 =
= =x+1.
=x+1.
又∵x是整数,
∴x+1是整数.
故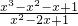 是整数.
是整数.
分析:(1)先将等式右边展开计算,再根据多项式恒等的性质,两边对应项系数相等,列出关于k的方程,从而求出k的值;
(2)把(1)中k的值代入,可将x3-x2-x+1因式分解,再进行分式的除法运算,可求出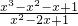 的结果,然后根据条件x是整数,即可得证.
的结果,然后根据条件x是整数,即可得证.
点评:本题主要考查了多项式乘多项式的法则,因式分解及分式的除法.由于多项式除以多项式的内容在初中教材大纲中不学习,故本题第二问有一定难度,属于竞赛题型.解决第一问的关键是根据多项式乘多项式的法则,利用两边对应项系数相等,列出关于k的方程;解决第二问的关键是利用(1)的结论,将多项式x3-x2-x+1因式分解.
所以x3-x2-x+1=x3+(k-1)x2-(k+1)x+1,
从而有k-1=-1,-k-1=-1,
解得k=0.
故所求k的值为0;
(2)由(1)知k=0,则x3-x2-x+1=(x-1)(x2-1)=(x-1)2(x+1),
∴
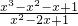 =
= =x+1.
=x+1.又∵x是整数,
∴x+1是整数.
故
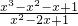 是整数.
是整数.分析:(1)先将等式右边展开计算,再根据多项式恒等的性质,两边对应项系数相等,列出关于k的方程,从而求出k的值;
(2)把(1)中k的值代入,可将x3-x2-x+1因式分解,再进行分式的除法运算,可求出
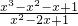 的结果,然后根据条件x是整数,即可得证.
的结果,然后根据条件x是整数,即可得证.点评:本题主要考查了多项式乘多项式的法则,因式分解及分式的除法.由于多项式除以多项式的内容在初中教材大纲中不学习,故本题第二问有一定难度,属于竞赛题型.解决第一问的关键是根据多项式乘多项式的法则,利用两边对应项系数相等,列出关于k的方程;解决第二问的关键是利用(1)的结论,将多项式x3-x2-x+1因式分解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目