Question

（1）已知恒等式x³-x²-x+1=（x-1）（x²+kx-1），求k的值；
（2）若x是整数，求证：

x3-x2-x+1

x2-2x+1

是整数．

Answer 1

（1）由题设知，（x-1）（x²+kx-1）=x³+（k-1）x²-（k+1）x+1，
所以x³-x²-x+1=x³+（k-1）x²-（k+1）x+1，
从而有k-1=-1，-k-1=-1，
解得k=0．
故所求k的值为0；
（2）由（1）知k=0，则x³-x²-x+1=（x-1）（x²-1）=（x-1）²（x+1），
∴

x3-x2-x+1

x2-2x+1

=

(x-1)2(x+1)

(x-1)2

=x+1．
又∵x是整数，
∴x+1是整数．
故

x3-x2-x+1

x2-2x+1

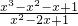是整数．