题目内容
已知：2（ax2-x3）+b（x2+ax）=ax3-3x2-cx是关于x的恒等式，求a+b+c的值．
分析：已知等式左边利用去括号法则去括号后，合并同类项得到最简结果，根据多项式相等的条件求出a，b及c的值，即可求出a+b+c的值．
解答：解：已知等式变形得：2ax2-2x3+bx2+abx=-2x3+（2a+b）x2+abx=ax3-3x2-cx，
则a=-2，2a+b=-3，ab=-c，
解得：a=-2，b=1，c=2，
则a+b+c=-2+1+2=1．
则a=-2，2a+b=-3，ab=-c，
解得：a=-2，b=1，c=2，
则a+b+c=-2+1+2=1．
点评：此题考查了整式的加减，涉及的知识有：去括号法则，以及合并同类项法则，熟练掌握法则是解本题的关键．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
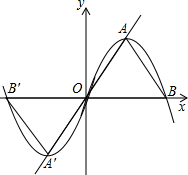已知：抛物线y=ax2+bx与x铀的一个交点为B，顶点A在直线y=
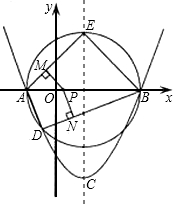已知：抛物线y=ax2+bx+c（a≠0），顶点C（1，-3），与x轴交于A，B两点，A（-1，0）．
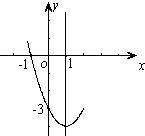7、已知，抛物线y=ax2+bx+c的部分图象如图，则下列说法①对称轴是直线x=1；②当-1＜x＜3时，y＜0；③a+b+c=-4；④方程ax2+bx+c+5=0无实数根．其中正确的有（ ）
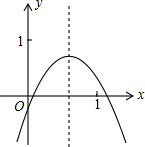已知=次函数y=ax2+bx+c的图象如图．则下列5个代数式：ac，a+b+c，4a-2b+c，2a+b，2a-b中，其值大于0的个数为
已知：抛物线y=ax2+bx+6与x轴交于A（1，0），B（3，0）．