ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§ΝΫΗωΒ»―ϋ÷±Ϋ«»ΐΫ«ΑεABCΚΆDEF”–“ΜΧθ±Ώ‘ΎΆ§“ΜΧθ÷±œΏl…œΘ§DE=2Θ§AB=1Θ°ΫΪ÷±œΏEB»ΤΒψEΡφ ±’κ–ΐΉΣ45ΓψΘ§ΫΜ÷±œΏAD”ΎΒψMΘ°ΫΪΆΦ1÷–ΒΡ»ΐΫ«ΑεABC―Ί÷±œΏlœρ”“ΤΫ“ΤΘ§…ηCΓΔEΝΫΒψΦδΒΡΨύάκΈΣkΘ°
Ϋβ¥πΈ ΧβΘΚ
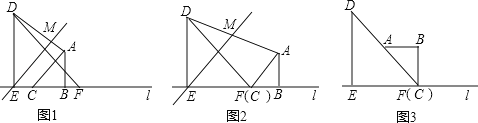
Θ®1Θ©ΔΌΒ±ΒψC”κΒψF÷ΊΚœ ±Θ§»γΆΦ2Υυ ΨΘ§Ω…ΒΟ![]() ΒΡ÷ΒΈΣ ΘΜ
ΒΡ÷ΒΈΣ ΘΜ
ΔΎ‘ΎΤΫ“ΤΙΐ≥Χ÷–Θ§![]() ΒΡ÷ΒΈΣ Θ®”ΟΚ§kΒΡ¥ζ ΐ Ϋ±μ ΨΘ©ΘΜ
ΒΡ÷ΒΈΣ Θ®”ΟΚ§kΒΡ¥ζ ΐ Ϋ±μ ΨΘ©ΘΜ
Θ®2Θ©ΫΪΆΦ2÷–ΒΡ»ΐΫ«ΑεABC»ΤΒψCΡφ ±’κ–ΐΉΣΘ§‘≠Χβ÷–ΒΡΤδΥϊΧθΦΰ±Θ≥÷≤Μ±δΘ°Β±ΒψA¬δ‘ΎœΏΕΈDF…œ ±Θ§»γΆΦ3Υυ ΨΘ§«κ≤Ι»ΪΆΦ–ΈΘ§ΦΤΥψ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®3Θ©ΫΪΆΦ1÷–ΒΡ»ΐΫ«ΑεABC»ΤΒψCΡφ ±’κ–ΐΉΣΠΝΕ»Θ§0ΘΦΠΝΓή90Θ§‘≠Χβ÷–ΒΡΤδΥϊΧθΦΰ±Θ≥÷≤Μ±δΘ°ΦΤΥψ![]() ΒΡ÷ΒΘ®”ΟΚ§kΒΡ¥ζ ΐ Ϋ±μ ΨΘ©Θ°
ΒΡ÷ΒΘ®”ΟΚ§kΒΡ¥ζ ΐ Ϋ±μ ΨΘ©Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΔΌ![]() =1ΘΜΔΎ
=1ΘΜΔΎ![]() =
=![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() Θ°Θ®3Θ©
Θ°Θ®3Θ©![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΔΌΗυΨίΧβ“βΩ…ΒΟEM¥Ι÷±ΤΫΖ÷DFΘ§÷±œΏAFΓΈEMΘ§¥”Εχ![]() ΉΣΜ·ΈΣ
ΉΣΜ·ΈΣ![]() Θ§ΦΧΕχΒΟ≥ωΫα¬έΘΜΔΎΖ¬’’ΔΌΒΡΥΦ¬ΖΫχ––«σΫβΦ¥Ω…ΘΜ
Θ§ΦΧΕχΒΟ≥ωΫα¬έΘΜΔΎΖ¬’’ΔΌΒΡΥΦ¬ΖΫχ––«σΫβΦ¥Ω…ΘΜ
Θ®2Θ©œ»≤Ι»ΪΆΦ–ΈΘ§Ν§Ϋ”AEΘ§Ζ÷±π«σ≥ωAMΦΑDMΒΡ÷ΒΘ§»ΜΚσΩ…»ΖΕ®±»÷ΒΘ°
Θ®3Θ©œ»Μ≠≥ωΆΦ–ΈΘ§»ΜΚσ÷ΛΟςΓςABGΓ’ΓςCBEΘ§ΦΧΕχΆΤ≥ωAGΓΈDEΘ§ΓςAGMΓΉΓςDEMΘ§άϊ”ΟœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…ΒΟ≥ω¥πΑΗΘ°
ΫβΘΚΘ®1Θ©ΔΌ»γΆΦΘ§
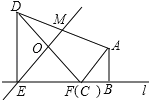
ΓΏΓœMEB=45ΓψΘ§ΓœAFB=45ΓψΘ§
ΓύEM¥Ι÷±«“ΤΫΖ÷DFΘ§AFΓΈEMΘ§
Γύ![]() =
=![]() =1ΘΜ
=1ΘΜ
ΔΎ»γΆΦ

”…ΔΌΩ…ΒΟ![]() =
=![]() =
=![]() =
=![]() =
=![]() ΘΜ
ΘΜ
Ȯ2ȩͧ۔AEȧ
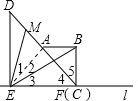
ΓΏΓςABCΘ§ΓςDEFΨυΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§DE=2Θ§AB=1Θ§
ΓύEF=2Θ§BC=1Θ§ΓœDEF=90ΓψΘ§Γœ4=Γœ5=45Γψ
ΓύDF=2![]() Θ§AC=
Θ§AC=![]() Θ§ΓœEFB=90ΓψΘ§
Θ§ΓœEFB=90ΓψΘ§
ΓύDF=2ACΘ§AD=![]() Θ§
Θ§
ΓύΒψAΈΣCDΒΡ÷–ΒψΘ§
ΓύEAΓΆDFΘ§EAΤΫΖ÷ΓœDEFΘ§
ΓύΓœMAE=90ΓψΘ§ΓœAEF=45ΓψΘ§AE=![]() Θ§
Θ§
ΓΏΓœBEM=45ΓψΘ§
ΓύΓœ1+Γœ2=Γœ3+Γœ2=45ΓψΘ§
ΓύΓœ1=Γœ3Θ§
ΓύΓςAEMΓΉΓςFEBΘ§
Γύ![]() Θ§
Θ§
ΓύAM=![]() Θ§
Θ§
ΓύDM=AD©¹AM=![]() Θ§
Θ§
Γύ![]() Θ°
Θ°
Θ®3Θ©ΙΐBΉςBEΒΡ¥ΙœΏΫΜ÷±œΏEM”ΎΒψGΘ§Ν§Ϋ”AGΓΔBGΘ§
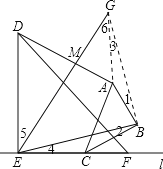 Θ§
Θ§
ΓύΓœEBG=90ΓψΘ§
ΓΏΓœBEM=45ΓψΘ§
ΓύΓœEGB=ΓœBEM=45ΓψΘ§
ΓύBE=BGΘ§
ΓΏΓςABCΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύBA=BCΘ§ΓœABC=90ΓψΘ§
ΓύΓœ1=Γœ2Θ§
ΓύΓςABGΓ’ΓςCBEΘ§
ΓύAG=EC=kΘ§Γœ3=Γœ4Θ§
ΓΏΓœ3+Γœ6=Γœ5+Γœ4=45ΓψΘ§
ΓύΓœ6=Γœ5Θ§
ΓύAGΓΈDEΘ§
ΓύΓςAGMΓΉΓςDEMΘ§
Γύ![]() Θ°
Θ°


