Question

【题目】数学兴趣小组的同学们对函数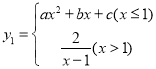的图象和性质进行了探究，已知时，函数的图象的对称轴为直线，顶点在轴上，与轴的交点坐标为，探究过程如下，请补充过程：

（1） ， ， ．

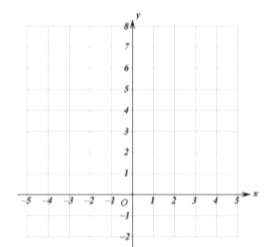
（2）在给出的平面直角坐标系中，画出函数图象，并写出这个函数的一条性质： ．

（3）进一步探究函数图象并解决问题：

①若有三个实数解，则的取值范围为： ．

②若函数的图象与该函数有三个交点，则的取值范围为： ．

Answer 1

【答案】（1），，；（2）图详见解析；性质不唯一，详见解析；（3）①；②

【解析】

（1）根据函数的图象的对称轴为直线，顶点在轴上，与轴的交点坐标为，得到关于a，b，c的方程组，解方程即可；

（2）根据题意，分别画出当x≤1，x＞1，时两部分的图像，并结合图像任意写出一条性质即可；

（3）①根据函数图像，画出，根据图像确定即可；

②与该函数有三个交点，根据函数图象，当的图象经过点时，此时最大，为；当的图象与二次函数的图象相切时，此为另一种临界情况，直线与图像有两个交点，联立方程组，，求出n，问题得解．

解：（1）由题意得的图象对称轴为直线，经过，

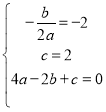则，解得

∴，，

（2）函数图像如图:

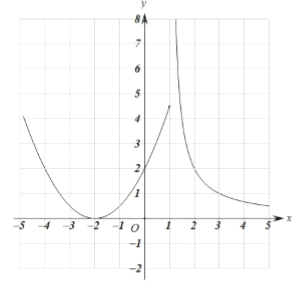
性质：当时，随的增大而减小；

当时，随的增大而增大；

当时，随的增大而减小．

当时，函数有最小值为0；

（3）①有三个解，即函数图像与直线有三个交点

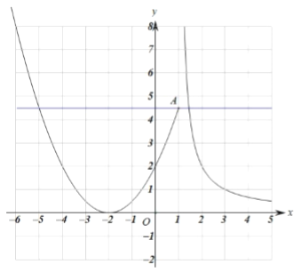
，当直线为直线或在其下方且在轴上方时，与函数图象有三个交点，

因此：

②

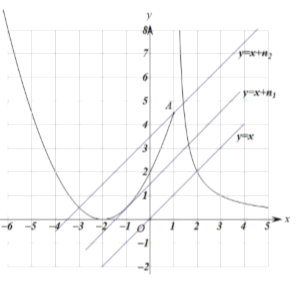
与该函数有三个交点，根据函数图象，

当的图象经过点时，此时最大，为；

当的图象与二次函数的图象相切时，此为另一种临界情况．

联立解析式，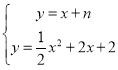

得，由，得，

因此：．