题目内容
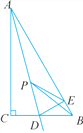
【题目】如图,在△ABC中,∠B=24°,∠ACB=104°,AD⊥BC于D,AE平分∠BAC,求∠DAE的度数.
【答案】解:在△ABC中,
∵∠BAC+∠B+∠ACB=180°,∠B=24°,∠ACB=104°,
∴∠BAC=180°﹣∠B﹣∠ACB=180°﹣24°﹣104°=52°.
∵AE平分∠BAC,
∴∠EAC=![]() ∠BAC=
∠BAC=![]() x52°=26°,
x52°=26°,
∵AD⊥BC,
∴∠ADC=90°,
∵∠ACB=104°,
∴∠ACD=180°﹣∠ACB=180°﹣104°=76°,
∴∠CAD=14°,
∴∠DAE=∠EAC+∠CAD=40°.
【解析】先根据三角形内角和定理求出∠BAC的度数,再根据角平分线的定义求出∠EAC的度数,由∠DAE=∠EAC+∠CAD即可得出结论.
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
【题目】某蔬菜经营户从蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如表:
蔬菜品种 | 西红柿 | 青椒 | 西兰花 | 豆角 |
批发价(元/㎏) | 3.6 | 5.4 | 8 | 4.8 |
零售价(元/㎏) | 5.4 | 8.4 | 14 | 7.6 |
请解答下列问题:
(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共300㎏,用去了1520元钱,这两种蔬菜当天全部售完一共赚了多少元钱?
(2)第二天,该经营户用1520元仍然批发西红柿和西兰花,要想当天全部售完后所赚钱数不少于1050元,则该经营户最多能批发西红柿多少㎏?