题目内容
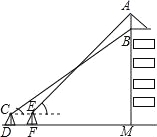
【题目】为了弘扬南开精神,我校将“允公允能,日新月异”的校调印在旗帜上,放置在教学楼的顶部(如图所示),小华在教学楼前空地上的点D处,用1米高的测角仪CD,从点C测得旗帜的底部B的仰角为37°,然后向教学楼正方向走了4.8米到达点F处,又从点E测得旗帜的顶部A的仰角为45°.若教学楼高BM=19米,且点A、B、M在同一直线上,求旗帜AB的高度(参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
【答案】宣传牌AB的高度约为1.2m
【解析】
试题分析:首先过点C作CN⊥AM于点N,则点C,E,N在同一直线上,设AB=x米,则AN=x+(19﹣1)=x+18(米),则在Rt△AEN中,∠AEN=45°,可得EN=AN=x+18,在Rt△BCN中,∠BCN=37°,BM=19m,可得tan∠BCN=![]() =0.75,则可得方程:
=0.75,则可得方程:![]() =
=![]() ,解此方程即可求得答案.
,解此方程即可求得答案.
试题解析:过点C作CN⊥AM于点N,则点C,E,N在同一直线上,
设AB=x米,则AN=x+(19﹣1)=x+18(米),
在Rt△AEN中,∠AEN=45°,
∴EN=AN=x+18,
在Rt△BCN中,∠BCN=37°,BM=19m,
∴tan∠BCN═![]() =0.75,
=0.75,
∴![]() =
=![]() ,
,
解得:x=1.2.
经检验:x=1.2是原分式方程的解.
答:宣传牌AB的高度约为1.2m.


练习册系列答案
相关题目