题目内容
【题目】如图,在![]() ABC中,过点C作CD//AB,E是AC的中点,连接DE并延长,交AB于点F,交CB的延长线于点G.连接AD、CF.
ABC中,过点C作CD//AB,E是AC的中点,连接DE并延长,交AB于点F,交CB的延长线于点G.连接AD、CF.
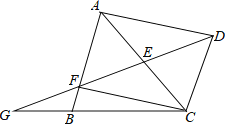
(1)求证:四边形AFCD是平行四边形;
(2)若GB=3,BC=6,BF=1,求AB的长.
【答案】(1)证明见详解;
(2)4
【解析】
(1)由E是AC的中点知AE=CE,由AB∥CD知∠AFE=∠CDE,据此根据“AAS”即可证△AEF≌△CED,从而得AF=CD,结合AB∥CD即可得证;
(2)证△GBF∽△GCD得![]() ,据此求得
,据此求得![]() ,由AF=CD及AB=AF+BF可得答案.
,由AF=CD及AB=AF+BF可得答案.
解:(1)∵E是AC的中点,
∴AE=CE,
∵AB∥CD,
∴∠AFE=∠CDE,
在△AEF和△CED中,
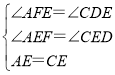 ,
,
∴△AEF≌△CED(AAS),
∴AF=CD,
又AB∥CD,即AF∥CD,
∴四边形AFCD是平行四边形;
(2)∵AB∥CD,
∴△GBF∽△GCD,
∴![]() ,
,
∵GB=3,BC=6,BF=1,
∴![]() ,
,
即:![]() ,
,
∵四边形AFCD是平行四边形,
∴![]() ,
,
∴![]() .
.

 习题精选系列答案
习题精选系列答案【题目】小明利用函数与不等式的关系,对形如![]() (
(![]() 为正整数)的不等式的解法进行了探究.
为正整数)的不等式的解法进行了探究.
(1)下面是小明的探究过程,请补充完整:
①对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如表格:
的图象可以得到如表格:
|
|
|
| + | ﹣ |
由表格可知不等式![]() 的解集为
的解集为![]() .
.
②对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如表表格:
的图象可以得到如表表格:
|
|
|
|
| + | ﹣ | + |
由表格可知不等式![]() 的解集为 .
的解集为 .
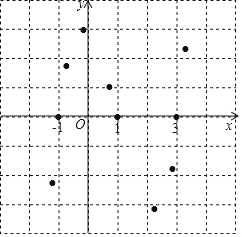
③对于不等式![]() ,请根据已描出的点画出函数
,请根据已描出的点画出函数![]() (x+1)的图象;
(x+1)的图象;
观察函数![]() 的图象补全下面的表格:
的图象补全下面的表格:
|
|
|
|
|
| + | ﹣ |
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
……
小明将上述探究过程总结如下:对于解形如![]() (
(![]() 为正整数)的不等式,先将
为正整数)的不等式,先将![]() 按从大到小的顺序排列,再划分
按从大到小的顺序排列,再划分![]() 的范围,然后通过列表格的办法,可以发现表格中
的范围,然后通过列表格的办法,可以发现表格中![]() 的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
(2)请你参考小明的方法解决下列问题:
①不等式![]() 的解集为 .
的解集为 .
②不等式![]() 的解集为 .
的解集为 .