��Ŀ����
��ͼ��1����ʾ��EΪ����ABCD�ı�AD��һ�㣬����P��Qͬʱ�ӵ�B��������P������BE��ED��DC�˶�����Cʱֹͣ����Q��BC�˶�����Cʱֹͣ�������˶����ٶȶ���1cm/�룮��P��Qͬʱ����t��ʱ����BPQ�����Ϊycm2����֪y��t�ĺ�����ϵͼ����ͼ��2��������OMΪ�����ߵ�һ���֣��������н��۴������




| A��AD��BE��5�M ������ | B��cos��ABE�� �� �� |
C����0��t��5ʱ�� | D���� ��ʱ����ABE�ס�QBP ��ʱ����ABE�ס�QBP |
B
�������������ͼ(2)��֪������P�����Eʱ��Q�����C��
�ߵ�P��Q���˶����ٶȶ���1cm/��
��BC=BE=5����AD=BE=5���ʽ���A��ȷ��
�֡ߴ�M��N�ı仯��2����ED=2
��AE=AD��ED=5��2="3,"
��Rt��ABE��

����cos��ABE��

�ʽ���B����
����P��PF��BC�ڵ�F��
��AD��BC�����AEB=��PBF����sin��PBF=sin��AEB=

��PF=PBsin��PBF=

�൱0��t��5ʱ��

����C��ȷ
��
 ʱ����P��CD�ϣ�
ʱ����P��CD�ϣ���ʱ��PD=
 -BE-ED=
-BE-ED= ��
��PQ=CD-PD=4-
 =
= 
��
 ,
, 
��

�֡ߡ�A=��Q=90�㣬���ABE�ס�QBP���ʽ���D��ȷ��
�������ѶȽϴؼ��������ն���ı仯���ɡ�

��ϰ��ϵ�д�
 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
�����Ŀ
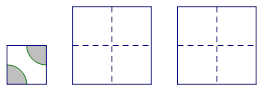



 ����������
���������� ���ڸ���ϣ�
���ڸ���ϣ�
 ��ʱ����ת
��ʱ����ת ��õ��������Σ�
��õ��������Σ�