题目内容
等腰三角形一腰上的高与另一腰的夹角是50°,则这个等腰三角形的底角为( )
| A、70° | B、20° | C、70°或20° | D、40°或140° |
分析:当该等腰三角形为钝角三角形时:底角=
(90°-50°)=20°,当该等腰三角形为锐角三角形时:底角=
[180°-(90°-50°)]=70°.
| 1 |
| 2 |
| 1 |
| 2 |
解答: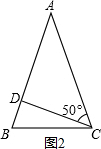
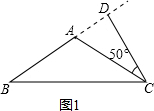 解:①如图1,当该等腰三角形为钝角三角形时,
解:①如图1,当该等腰三角形为钝角三角形时,
∵一腰上的高与另一腰的夹角是50°,
∴底角=
(90°-50°)=20°,
②如图2,当该等腰三角形为锐角三角形时,
∵一腰上的高与另一腰的夹角是50°,
∴底角=
[180°-(90°-50°)]=70°.
故选C.

 解:①如图1,当该等腰三角形为钝角三角形时,
解:①如图1,当该等腰三角形为钝角三角形时,∵一腰上的高与另一腰的夹角是50°,
∴底角=
| 1 |
| 2 |
②如图2,当该等腰三角形为锐角三角形时,
∵一腰上的高与另一腰的夹角是50°,
∴底角=
| 1 |
| 2 |
故选C.
点评:本题主要考查等腰三角形的性质,垂直的性质,关键在于分情况进行分析,认真的进行计算.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目