题目内容
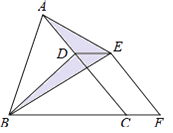
【题目】如图,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BE.
求证:BD=2CE.
【答案】证明:延长CE交BA的延长线于点F,如图所示.
∵CE⊥BE,
∴∠BEC=∠BEF=90°.
又∵∠1=∠2,
∴∠F=∠BCE,
∴BC=BF,
∴CE=FE= ![]() CF,
CF,
即CF=2CE.
∵∠F+∠2=90°,∠F+∠ACF=90°,
∴∠2=∠ACF.
又∵AB=AC,∠BAD=∠CAF=90°,
∴△BDA≌△CFA(ASA).
∴BD=CF.
∴BD=2CE 。
【解析】延长CE交BA的延长线于点F,如图所示.根据垂直的定义得出∠BEC=∠BEF=90° ,根据三角形的内角和得出∠F=∠BCE,根据等角对等边得出BC=BF,从而根据等腰三角形的三线合一得出CE=FE= ![]() CF, 即CF=2CE ,根据同角的余角相等得出∠2=∠ACF,然后利用ASA判断出BD=CF,根据等量代换得出BD=2CE 。
CF, 即CF=2CE ,根据同角的余角相等得出∠2=∠ACF,然后利用ASA判断出BD=CF,根据等量代换得出BD=2CE 。

练习册系列答案
相关题目