题目内容
 如图,点P是等腰△ABC的底边BC上的点,以AP为腰在AP的两侧分别作等腰△AFP和等腰△AEP,且∠APF=∠APE=∠B,PF交AB于点M,PE交AC于点N,连接MN.
如图,点P是等腰△ABC的底边BC上的点,以AP为腰在AP的两侧分别作等腰△AFP和等腰△AEP,且∠APF=∠APE=∠B,PF交AB于点M,PE交AC于点N,连接MN.求证:MN∥BC.
分析:由已知条件可以得出AF=AP,∠F=∠APN,∠FAM=∠PAN,可以得出△AFM≌△APN,得到AM=AN,从而得出结论.
解答:证明:∵△ABC、△AFP和△AEP是等腰三角形,
∴AF=AP,∠F=∠APN,∠FAM=∠PAN,
在△AFM和△APN中,
∵
∴△AFM≌△APN(ASA),
∴AM=AN.
∴∠AMN=∠B,
∴MN∥BC.
∴AF=AP,∠F=∠APN,∠FAM=∠PAN,
在△AFM和△APN中,
∵
|
∴△AFM≌△APN(ASA),
∴AM=AN.
∴∠AMN=∠B,
∴MN∥BC.
点评:本题考查了等腰三角形的性质,全等三角形的判定与性质的运用.

练习册系列答案
相关题目
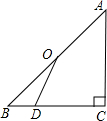 已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.
已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.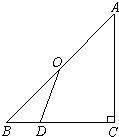 27、附加题:已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.
27、附加题:已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点. 11、如图,点D是等腰直角△ABC斜边AB上的点,将△ACD绕点C逆时针旋转,使它与△BCD′重合,则∠D′BA=
11、如图,点D是等腰直角△ABC斜边AB上的点,将△ACD绕点C逆时针旋转,使它与△BCD′重合,则∠D′BA=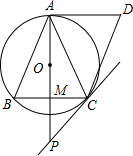 如图,点O是等腰△ABC的外心,AD是圆O的切线,切点为A,过点C作CD≡∥AB,交AD于点D.连接AO并延长交BC于点M,连接AD,交过点C的直线于点P,且∠BCP=∠ACD.
如图,点O是等腰△ABC的外心,AD是圆O的切线,切点为A,过点C作CD≡∥AB,交AD于点D.连接AO并延长交BC于点M,连接AD,交过点C的直线于点P,且∠BCP=∠ACD.