��Ŀ����
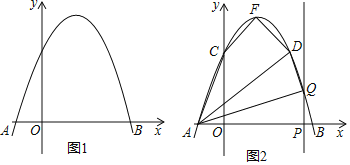
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��A�ڵ�һ���ޣ���B��x���������ϣ�AO=AB��OB=4��tan��AOB=2����C���߶�OA���е㣮
��1�����C�����ꣻ
��2������P��x���ϵ�һ�����㣬ʹ�á�APO=��CBO��������y=ax2+bx������A����P�������������ߵĺ�������ʽ��
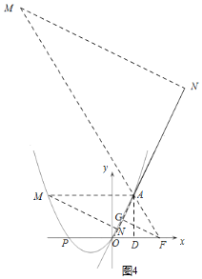
��3���ڣ�2���������£���M��������ͼ���ϵ�һ�����㣬��MΪԲ�ĵ�Բ��ֱ��OA���У��е�Ϊ��N����A����ֱ��MN�ĶԳƵ�Ϊ��D������̽�����Ƿ���������ĵ�M��ʹ����MAD�ס�AOB�������ڣ���ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
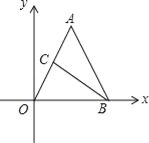
���𰸡���1��C������Ϊ��1��2������2��y=��![]() x2+
x2+![]() x��y=
x��y=![]() x2+
x2+![]() x����3�����������ĵ�M��6��4����10��-
x����3�����������ĵ�M��6��4����10��-![]() ����10��20����6��4����ʹ����MAD�ס�AOB
����10��20����6��4����ʹ����MAD�ס�AOB
��������
��1������A��AD��OB�ڵ�D������C��CE��OB�ڵ�E���ɵ��������ε����ʿɵ�OD=![]() OB=2������tan��AOB=2���ɵ�AD=4��������λ�ߵ����ʼ������C�����ꣻ��2���ɣ�1���ɵ�A������͡�CBE������ֵ�������ɵá�APO������ֵ���������PD�ij�������PD=|x��2|�������P�����꣬��A��P�����������y=ax2+bx�������a��b��ֵ�����ɵ������߽���ʽ����3������MAD�ס�AOB�����MAN=��AOB�����ڣ�2���������������߽���ʽ�����Է�����������ۣ������е�N�IJ�ȷ���ԣ����Ե�N��λ�������֣�һ���ǵ�N�ڵ�A���Ϸ�����һ���ǵ�N�ڵ�A���·���
OB=2������tan��AOB=2���ɵ�AD=4��������λ�ߵ����ʼ������C�����ꣻ��2���ɣ�1���ɵ�A������͡�CBE������ֵ�������ɵá�APO������ֵ���������PD�ij�������PD=|x��2|�������P�����꣬��A��P�����������y=ax2+bx�������a��b��ֵ�����ɵ������߽���ʽ����3������MAD�ס�AOB�����MAN=��AOB�����ڣ�2���������������߽���ʽ�����Է�����������ۣ������е�N�IJ�ȷ���ԣ����Ե�N��λ�������֣�һ���ǵ�N�ڵ�A���Ϸ�����һ���ǵ�N�ڵ�A���·���
��1������A��AD��OB�ڵ�D������C��CE��OB�ڵ�E��
��AO=AB��
��AD����AOB�����ߣ�
��OD=![]() OB=2��
OB=2��
��tan��AOB=2��
��![]() =2��
=2��
��AD=4��
��CE��AD����C��AO���е㣬
��CE����AOD����λ�ߣ�
��CE=![]() AD=2��OE=
AD=2��OE=![]() OD=1��
OD=1��
��C��������1��2����
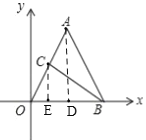
��2���ɣ�1����֪��CE=2��BE=3��A������Ϊ��2��4����
��tan��CBE=![]() =
=![]() ��
��
�ߡ�APO=��CBO��
��tan��APO=tan��CBO=![]() ��
��
��![]() =
=![]() ��
��
��PD=6��
��P��������x��0����
��D��2��0����
��PD=|x��2|��
��|x��2|=6��
��x=8��x=��4��
��P��8��0����4��0����
��P������Ϊ��8��0��ʱ����A��2��4���ͣ�8��0������y=ax2+bx��
��![]() ��
��
��ã�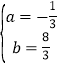 ��
��
�������ߵĽ���ʽΪ��y=��![]() x2+
x2+![]() x��
x��
��P������Ϊ����4��0��ʱ����A��2��4����P����4��0������y=ax2+bx��
��![]() ����ã�
����ã�![]() ��
��
�������ߵĽ���ʽΪ��y=![]() x2+
x2+![]() x��
x��
���������������ߵĽ���ʽΪ��y=��![]() x2+
x2+![]() x��y=
x��y=![]() x2+
x2+![]() x��
x��
��3����MΪԲ�ģ�NΪ�е㣬
��MN��OA��
��D����A�����MN�ĶԳƵ㣬
���MAD�ǵ��������Σ�MA=MD
����MAD�ס�AOBʱ��
�ߡ�AOB�ǵ��������Σ�
���MAD=��AOB��
�������ߵĽ���ʽΪy=��![]() x2+
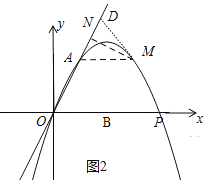
x2+![]() xʱ����ͼ2��
xʱ����ͼ2��
������N��A���Ϸ�ʱ����ʱ��MAN=��AOB��
��AM��x�ᣬ
��M��������Ϊ4��
���y=4����y=��![]() x2+
x2+![]() x��
x��
��ã�x=2����ȥ����x=6��
��M��������6��4����
�ڵ���N�ڵ�A���·�ʱ����ʱ��MDA=��AOB��
��DM��x�ᣬ
����A��AE��DM�ڵ�E������x���ڵ�F����D�������Ϊa��
��DE=2-a��
��tan��MDA=tan��AOB=2��
��AE=2DE=4-2a��
���M��������Ϊ2a��
���ɹ��ɶ�����֪��AD=![]() ��2-a����OA=2
��2-a����OA=2![]() ��
��
��![]() ����
����![]() ��
��
��DM=![]() ��
��
��M�ĺ�����Ϊx��
��x-a=![]()
��x=![]() ��
��
��M��![]() ��2a��
��2a��
��M��![]() ��2a������y=��
��2a������y=��![]() x2+
x2+![]() x��
x��
�ã�2a=-![]() ��(
��(![]() )2+
)2+![]() ��(
��(![]() )
)
��ã�a=2��a=-![]() ��
��
�൱a=2ʱ��M��2��4����ȥ
��a=-![]() ʱ��M��10��-
ʱ��M��10��-![]() ��
��
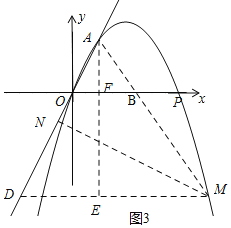
�������ߵĽ���ʽΪy=![]() x2+
x2+![]() xʱ����ͼ4��
xʱ����ͼ4��
����N�ڵ�A���Ϸ�ʱ����ʱ��MAN=��AOB��
�ӳ�MA��x���ڵ�F��
�ߡ�MAN=��OAF��
���AOB=��OAF��
��FA=FO��
����F��FG��OA�ڵ�G��
��A��2��4����
���ɹ��ɶ�������ã�AO=2![]() ��
��
��OG=![]() AO=
AO=![]() ��
��
��tan��AOB=![]()
��GF=2![]() ��
��
���ɹ��ɶ�������ã�OF=5��
��F������Ϊ��5��0������ֱ��MA�Ľ���ʽΪ��y=mx+n��
��A��2��4����F��5��0������y=mx+n��
��![]() ��
��
��ã�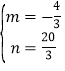 ��
��
��ֱ��MA�Ľ���ʽΪ��y=��![]() +
+![]() ��
��
����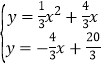 ��
��
���ã�x=2����ȥ����x=��10��
��x=��10����y=��![]() +
+![]() ��
��
��y=20��
��M����10��20����
����N�ڵ�A���·�ʱ����ʱ��MAN=��AOB��
��AM��x�ᣬ
��M��������Ϊ4��
��y=4����y=![]() x2+
x2+![]() x��
x��
��x=��6��x=2����ȥ����
��M����6��4����
�������������������ĵ�M��6��4����10��-![]() ����10��20����6��4����ʹ�á�MAD�ס�AOB
����10��20����6��4����ʹ�á�MAD�ס�AOB

����Ŀ���л�������ԴԶ�������л����֣�Ԣ����㣬Ϊ�˴������㴫ͳ�Ļ���ijУ��ί��֯��һ��ȫУ3000��ѧ���μӵ���������д�����������������в���ѧ���ijɼ���������50�֣�Ϊ�˸��õ��˽Ȿ�δ����ijɼ��ֲ�����������ȡ������200��ѧ���ijɼ����ɼ�xȡ�������ܷ�100�֣���Ϊ���������������õ����в�������ͳ��ͼ����
�ɼ�x/�� | Ƶ�� | Ƶ�� |
50��x��60 | 10 | 0.05 |
60��x��70 | 20 | 0.10 |
70��x��80 | 30 | b |
80��x��90 | a | 0.30 |
90��x��100 | 80 | 0.40 |
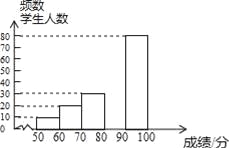
�����������Ϣ������������⣺
��1��a=______��b=______��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3����α����ɼ�����λ��������_____________�����Σ�
��4�����ɼ���90�����ϣ�����90�֣���Ϊ�������ȣ����У�μ���α�����3000��ѧ���гɼ���������Լ�ж����ˣ�