Question

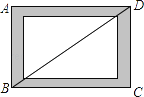
【题目】如图，已知△ABC是⊙O的内接三角形，AB为⊙O的直径，OD⊥AB于点O，且∠ODC=2∠A．

（1）求证：CD是⊙O的切线；

（2）若AB=6，，求CD的长．

Answer 1

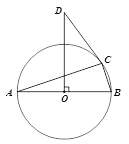
【答案】（1）证明见解析（2）4

【解析】分析：(1)、连接OC，根据等腰三角形的性质得出∠BOC=2∠A，结合∠ODC=2∠A得出∠ODC=∠BOC，根据OD⊥AB得出∠ODC+∠COD=90°，即∠OCD=90°，从而得出答案；(2)、过点C作CH⊥AB于点H，根据圆周角的性质以及Rt△ABC的勾股定理得出BC的值，根据Rt△BCH的勾股定理得出BH、CH和OH的长度，然后根据△DOC和△OCH相似得出答案．

详解：(1)证明：如图，连接OC，

∵△ABC是⊙O的内接三角形，∴OA=OC，∴∠A=∠ACO， ∴∠BOC=2∠A.

又∵∠ODC=2∠A，∴∠ODC=∠BOC， ∵OD⊥AB，即∠BOC+∠COD=90°，∴∠ODC+∠COD=90°,

∴∠OCD=90°, 即CD⊥OC，又OC是⊙O的半径，∴CD是⊙O的切线.

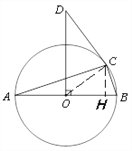
(2)如图，过点C作CH⊥AB于点H， ∵AB为⊙O的直径，点C在⊙O上，∴∠ACB=90°,

又∠CBH＝∠ABC，∴∠BCH＝∠A， 在Rt△ABC中，，

∴，则，，

又在Rt△BCH中，，∴，

则，∴，， ∵OB＝OC＝3，∴，

又∵Rt△DOC∽Rt△OCH， ∴则 .