��Ŀ����
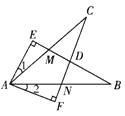
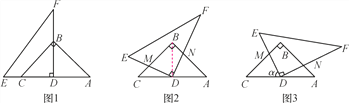
����Ŀ��(12��)��ͼ1����֪Rt��ABC����AB��BC��AC��2����һ�麬30���ǵ����ǰ�DEF��ֱ�Ƕ���D����AC���е���(ֱ�����ǰ�Ķ�ֱ�DZ�ΪDE����ֱ�DZ�ΪDF)����C��DE������B��DF�ϣ�
(1)���ص�������BCD�������
(2)��ͼ2����ֱ�����ǰ�DEF��D�㰴˳ʱ�뷽����ת30����DE��BC�ڵ�M��DF��AB�ڵ�N.
����֤��DM��DN��
���ڴ��������ص����ֵ�����ᷢ���仯���������仯��������ص����ֵ���������������仯����˵�����ɣ�
(3)��ͼ3����ֱ�����ǰ�DEF��D�㰴˳ʱ�뷽����ת����(0������90)��DE��BC�ڵ�M��DF��AB�ڵ�N����DM��DN�Ľ����Գ������ص����ֵ���������(��ֱ��д������������Ҫ˵������)
���𰸡�(1) ![]() (2)�ټ����� �ڲ��� (3) �Գ���������
(2)�ټ����� �ڲ��� (3) �Գ���������
���������������:(1)�ص�������BCD��һ������ֱ��������,�����ֱ�DZ�,�������,
(2)����BD,���ݵ���ֱ�������ε����ʿɵ�: ��C=��ABD=45��,CD=BD,
����Ϊ��CDM+��BD M=��BDN+��BDM=90��,���ԡ�CDM =��BDN,
���ݽDZ߽ǿ����ж���CDM�ա�BDN,�����ص������ı��ε����������BCD�����,���������,
(3)����BD,����(2)�еĽ���˼·��֤��CDM�ա�BDN,�����ص������ı��ε����������BCD�����,���������.
�������: (1)��AB=BC,AC=2,D��AC���е�,
��CD=BD=![]() AC=1,BD��AC.
AC=1,BD��AC.
��S��BCD��![]() CD��BD=
CD��BD=![]() ��1��1=
��1��1=![]() .
.
(2)��֤��:����BD,��BD��ֱƽ��AC.
��BD=CD,��C=��NBD=45��,
�֡ߡ�CDM=��BDN,
���CDM�ա�BDN(ASA)��
��DM=DN.
���ɢ�֪��CDM�ա�BDN����S�ı���BNDM��S��BCD��![]() �������������ص����ֵ�������䣬Ϊ
�������������ص����ֵ�������䣬Ϊ![]() .
.
(3)DM=DN�Ľ����Գ���,�ص����ֵ���������.