题目内容
 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连接EC、CD.
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连接EC、CD.
(1)求证:直线AB是⊙O的切线;
(2)试猜想BC,BD,BE三者之间的等量关系,并加以证明.
 (1)证明:如图,连接OC.
(1)证明:如图,连接OC.∵OA=OB,CA=CB,
∴OC⊥AB.
∴AB是⊙O的切线;
(2)解:BC2=BD•BE.
证明:∵ED是直径,
∴∠ECD=90°,
∴∠E+∠EDC=90°,
又∵∠BCD+∠OCD=90°,∠OCD=∠ODC,
∴∠BCD=∠E.
又∵∠CBD=∠EBC,
∴△BCD∽△BEC.
∴
 ,
,∴BC2=BD•BE.
分析:(1)连接OC,根据OA=OB,CA=CB,可以证明OC⊥AB,利用切线的判定定理,经过半径的外端,并且垂直于这条半径的直线是圆的切线,得到AB是⊙O的切线;
(2)根据ED是直径,直径所对的圆周角是直角,以及圆的切线垂直于过切点的半径,利用等量代换得到∠E=∠BCD,又∠B公共,可以证明△BCD∽△BEC,然后利用相似三角形的性质,对应线段的比相等得到BC2=BD•BE.
点评:本题考查了切线的判定,(1)利用等腰三角形底边上的中线也是底边上的高,得到OC⊥AB,证明AB是⊙O的切线.(2)根据题意证明两个三角形相似,利用相似三角形的性质,得到线段BC,BD和BE的数量关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
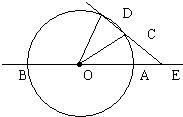 7、如图,直线AB经过⊙O的圆心,与⊙O相交于A、B两点,点C在⊙O上,且∠AOC=30度.点E是直线AB上的一个动点(与点O不重合),直线EC交⊙O于D,则使DE=DO的点E共有( )
7、如图,直线AB经过⊙O的圆心,与⊙O相交于A、B两点,点C在⊙O上,且∠AOC=30度.点E是直线AB上的一个动点(与点O不重合),直线EC交⊙O于D,则使DE=DO的点E共有( )
 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,连接EC、CD.
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,连接EC、CD.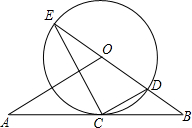 CD.
CD. 合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S.
合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S.