题目内容
如图,在□ABCD中,点M为边AD的中点,过点C作AB的垂线交AB于点E,连接ME.
(1)若AM=2AE=4,∠BCE=30°,求□ABCD的面积;
(2)若BC=2AB,求证:∠EMD=3∠MEA.

(1)若AM=2AE=4,∠BCE=30°,求□ABCD的面积;
(2)若BC=2AB,求证:∠EMD=3∠MEA.

(1)24 ;(2)证明见解析.
;(2)证明见解析.
 ;(2)证明见解析.
;(2)证明见解析.试题分析:(1)利用平行四边形的性质以及直角三角形的性质得出CE的长,进而得出答案;
(2)利用全等三角形的判定得出△AEM≌△DNM(ASA),进而得出∠EMC=2∠N=2∠AEM,再求出∠EMD=∠EMC+∠CMD=2∠AEM+∠AEM,进而得出答案.
(1)解:∵M为AD的中点,AM=2AE=4,
∴AD=2AM=8.在?ABCD的面积中,BC=CD=8,
又∵CE⊥AB,∴∠BEC=90°,∵∠BCE=30°,∴BE=
 BC=4,
BC=4,∴AB=6,CE=4
 ,
,∴?ABCD的面积为:AB×CE=6×4
 =24
=24 ;
;(2)证明:延长EM,CD交于点N,连接CM.

∵在?ABCD中,AB⊥CD,∴∠AEM=∠N,
在△AEM和△DNM中
∵
 ,
,∴△AEM≌△DNM(ASA),
∴EM=MN,
又∵AB∥CD,CE⊥AB,
∴CE⊥CD,
∴CM是Rt△ECN斜边的中线,
∴MN=MC.∴∠N=∠MCN,
∴∠EMC=2∠N=2∠AEM.
∵在平行四边形ABCD中,BC=AD=2DM,BC=2AB=2CD,
∴DC=MD,
∴∠DMC=∠MCD=∠N=∠AEM,
∴∠EMD=∠EMC+∠CMD=2∠AEM+∠AEM,
即∠EMD=3∠AEM.

练习册系列答案
相关题目

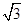


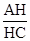 的值为 .
的值为 .