题目内容
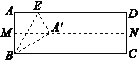
【题目】如图,四边形ABCD是正方形,E是线段CD上的点,将△ADE沿AE对折得到△AFE,直线EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)当DE是CD的一半时,求∠EAG的度数.

【答案】(1)证明见解析(2)45°
【解析】
(1)由正方形的性质和折叠的性质易得AB=AD=AF,∠B=∠D=∠AFE=∠AFG=90°,这样结合AG=AG即可由“HL”证得△ABG≌△AFG;
(2)由折叠的性质可得∠EAF=∠EAD,由(1)中所当△ABG≌△AFG可得∠FAG=∠BAG,这样结合在正方形ABCD中,∠BAD=90°即可得到∠EAG=∠EAF+∠GAF=![]() ∠BAD=45°.
∠BAD=45°.
(1)∵四边形ABCD为正方形,
∴AB=AD,∠B=∠D=90°.
∵将△ADE沿AE对折得到△AFE,
∴AF=AD=AB,∠AFE=∠D=90°.
在Rt△ABG和Rt△AFG中:![]() ,
,
∴Rt△ABG≌Rt△AFG(HL).
(2)∵由(1)可知:△ABG≌△AFG,
∴∠GAF=∠GAB.
∵△AFE是由△ADE沿AE折叠得到的,
∴∠EAF=∠EAD,
∵在正方形ABCD中,∠BAD=90°,
∴∠EAG=∠EAF+∠GAF=![]() ×90°=45°.
×90°=45°.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目