题目内容
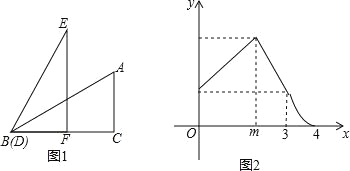
【题目】如图1,将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,得到△ABD和△ECF,固定△ABD,并把△ABD与△ECF叠放在一起.
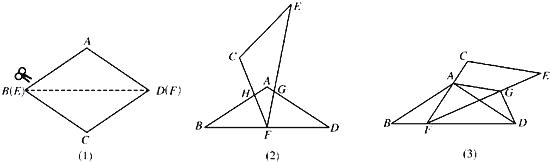
(1)操作:如图2,将△ECF的顶点F固定在△ABD的BD边上的中点处,△ECF绕点F在BD边上方左右旋转,设旋转时FC交BA于点H(H点不与B点重合),FE交DA于点G(G点不与D点重合).
求证:BHGD=BF2
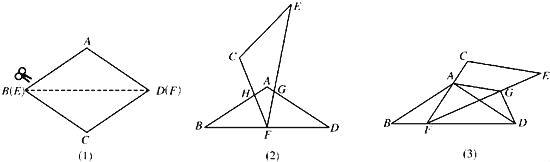
(2)操作:如图3,△ECF的顶点F在△ABD的BD边上滑动(F点不与B、D点重合),且CF始终经过点A,过点A作AG∥CE,交FE于点G,连接DG.
探究:FD+DG= .请予证明.
【答案】(1)证明见解析(2)BD
【解析】
试题分析:(1)根据菱形的性质以及相似三角形的判定得出△BFH∽△DGF,即可得出答案;
(2)利用已知以及平行线的性质证明△ABF≌△ADG,即可得出FD+DG的关系.
试题解析:(1)∵将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,
∴∠B=∠D,
∵将△ECF的顶点F固定在△ABD的BD边上的中点处,△ECF绕点F在BD边上方左右旋转,
∴BF=DF,
∵∠HFG=∠B,
又∵∠HFD=∠HFG+∠GFD=∠B+∠BHF
∴∠GFD=∠BHF,
∴△BFH∽△DGF,
∴![]() ,
,
∴BHGD=BF2;
(2)∵AG∥CE,
∴∠FAG=∠C,
∵∠CFE=∠CEF,
∴∠AGF=∠CFE,
∴AF=AG,
∵∠BAD=∠C,
∴∠BAF=∠DAG,
又∵AB=AD,
∴△ABF≌△ADG,
∴FB=DG,
∴FD+DG=BD,
故答案为:BD.

练习册系列答案
相关题目