��Ŀ����
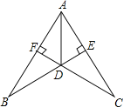
����Ŀ������ABC�У���ACB=90�㣬AC=BC��ֱ��MN������C����AD��MN��D��BE��MN��E��
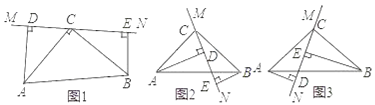
��1����ֱ��MN�Ƶ�C��ת��ͼ1��λ��ʱ����֤���١�ADC�ա�CEB����DE=AD+BE��
��2����ֱ��MN�Ƶ�C��ת��ͼ2��λ��ʱ����֤��DE=AD��BE��
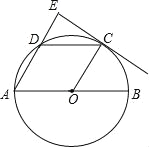
��3����ֱ��MN�Ƶ�C��ת��ͼ3��λ��ʱ������DE��AD��BE���������ĵ�����ϵ����д�����������ϵ��������֤����
���𰸡���1��֤������������2��֤������������3��DE=BE��AD��
����������1������֪AC=BC����ADC=��CEB=90�㣬���û����ϵ��֤��DAC=��ECB����֤��ACD�ա�CBE����AD=CE��CD=BE����AD+BE=CE+CD=DE����2����ʱ�����С�ACD�ա�CBE��AD=CE��CD=BE�������߶εĺͲ��ϵ��DE=AD-BE��
֤������1���ߡ�ADC=��ACB=��BEC=90�㣬
���CAD+��ACD=90�㣬��BCE+��CBE=90�㣬��ACD+��BCE=90�㣮
���CAD=��BCE��
��AC=BC��
���ADC�ա�CEB��
��CE=AD��CD=BE��
��DE=CE+CD=AD+BE��
��2��DE=AD��BE
֤�����ߡ�ADC=��CEB=��ACB=90�㣬
���ACD=��CBE��
�֡�AC=BC��
���ACD�ա�CBE��
��CE=AD��CD=BE��
��DE=CE��CD=AD��BE��
��3��DE=BE��AD����AD=BE��DE��BE=AD+DE�ȣ���
��֤�á�ACD�ա�CBE��
��AD=CE��DC=BE��
��DE=CD- CE =BE��AD��
���㾦�����⿼��������ת��Ѱ��֤��������ȫ�ȵ��������ؼ�������ȫ�������ζ�Ӧ�߶���ȣ����й��߶ν���ת����

����Ŀ�������о��е���ѧ�������ᄊ�˶����ϣ��μ��������ߵ�15���˶�Ա�ijɼ����±���ʾ��
�ɼ���m�� | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
���� | 1 | 2 | 4 | 3 | 3 | 2 |
��Щ�˶�Ա���߳ɼ�����λ���������ֱ��ǣ�������
A. 1.70��1.65 B. 1.70��1.70 C. 1.65��1.70 D. 3��4