题目内容
李老师从家到学校以每分钟
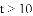
A. 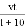 米 B.
米 B. 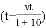 米 C.
米 C. 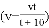 米 D.
米 D. 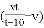 米
米
练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
题目内容
李老师从家到学校以每分钟
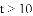
A. 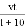 米 B.
米 B. 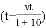 米 C.
米 C. 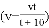 米 D.
米 D. 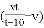 米
米
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案