题目内容
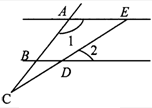 2、如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C的度数是( )
2、如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C的度数是( )分析:由AE∥BD,可求得∠CBD的度数,又由∠CBD=∠2(对顶角相等),求得∠CDB的度数,再利用三角形的内角和等于180°,即可求得答案.
解答:解:∵AE∥BD,∠1=130°,∠2=30°,
∴∠CBD=∠1=130°,∠CDB=∠2=30°,
∴∠C=180°-∠CBD-∠CDB=180°-130°-30°=20°.
故选B.
∴∠CBD=∠1=130°,∠CDB=∠2=30°,
∴∠C=180°-∠CBD-∠CDB=180°-130°-30°=20°.
故选B.
点评:此题考查了平行线的性质,对顶角相等以及三角形内角和定理.解题的关键是注意数形结合思想的应用.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
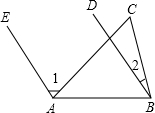 如图,已知AE∥BD,∠1=3∠2,∠2=28度.求
如图,已知AE∥BD,∠1=3∠2,∠2=28度.求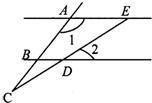 13、如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C=
13、如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C=
