题目内容
【题目】
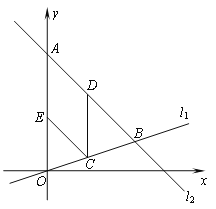
如图,在平面直角坐标系内,点A的坐标为(0,24 ),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
(1)求直线l1,l2的表达式.
(2)点C为线段OB上一动点(点C不与点O,B重合),CD∥y轴交直线l2于点D,CE∥l2交y轴于点E.
①若点C的横坐标为m,求四边形AECD的面积S与m的函数关系式;
②当S最大时,求出点C的坐标.
【答案】(1)直线l1的表达式为y=![]() x.直线l2的表达式为y=-x+24.(2)S=(-
x.直线l2的表达式为y=-x+24.(2)S=(-![]() m+24)m=-
m+24)m=-![]() m2+24m(0<m<18).点C的坐标为(9,3).
m2+24m(0<m<18).点C的坐标为(9,3).
【解析】
试题分析:(1)分别设出直线l1,l2的表达式,由点A、B的坐标利用待定系数法即可求出结论;
(2)①根据直线l1的解析式可找出点C的坐标,根据直线l2的表达式可找出点D的坐标,结合CD∥y轴,CE∥l2可得出四边形AECD为平行四边形,再由点C、D的坐标利用平行四边形的面积公式即可得出结论;
②根据二次函数的性质找出S取最值时m的值,由此即可得出点C的坐标.
试题解析:(1)设直线l1的表达式为y=k1x,
将点B(18,6)代入y=k1x中得:18k1=6,
解得:k1=![]() ,
,
∴直线l1的表达式为y=![]() x.
x.
设直线l2的表达式为y=k2x+b,
将点A(0,24),B(18,6)代入y=k2x+b中得:
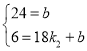 ,
,
解得:![]() ,
,
∴直线l2的表达式为y=-x+24.
(2)①将x=m代入y=![]() x得:y=
x得:y=![]() m,
m,
∴点C的坐标为(m,![]() m)(0<m<18).
m)(0<m<18).
∵CD∥y轴,
∴D点的横坐标也为m,
将x=m代入y=-x+24中得:y=-m+24,
∴点D的坐标为(m,-m+24),
∴CD=(-m+24)-![]() m=-
m=-![]() m+24.
m+24.
∵CD∥y轴,CE∥l2,
∴四边形AECD为平行四边形.
∵C(m,![]() m),
m),
∴CD边上的高为m,
∴S=(-![]() m+24)m=-
m+24)m=-![]() m2+24m(0<m<18).
m2+24m(0<m<18).
②由S=-![]() m2+24m得:-
m2+24m得:-![]() =9,
=9,
∴当m=9时,S最大,
此时![]() m=3.
m=3.
∴当S最大时,点C的坐标为(9,3).

 优等生题库系列答案
优等生题库系列答案