题目内容
【题目】把一个长为![]() 、宽为
、宽为![]() 的长方形(
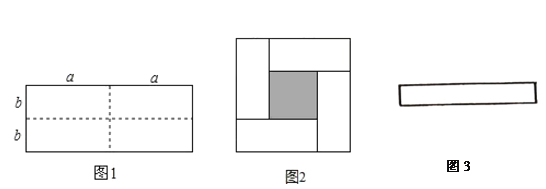
的长方形(![]() ),沿图1中虚线用剪刀分成四块相同的小长方形,并将
),沿图1中虚线用剪刀分成四块相同的小长方形,并将![]() 块小长方形彼此不重叠拼成一个正方形(如图2)
块小长方形彼此不重叠拼成一个正方形(如图2)
(1)图2中大正方形的边长为 ;小正方形(阴影部分)的边长为 .(用含![]() 的代数式表示).
的代数式表示).
(2)利用图2存在的面积关系,直接写出下列三个代数式![]() 之间的等量关系: .
之间的等量关系: .
(3)如图3,已知长方形的周长为![]() ,面积为
,面积为![]() ,试求该长方形长与宽的差.
,试求该长方形长与宽的差.
【答案】(1)a+b,a-b;(2)(a+b)2-4ab=(a-b)2;(3)![]() .
.
【解析】
(1)由操作可知,图1中每个小长方形的长为a,宽为b,根据图2求出边长即可;
(2)由每个小长方形的长为a,宽为b,可得每个小长方形的面积为ab,根据图2中阴影部分的面积表示即可得解;
(3)设长方形长为2a,宽为2b,由长方形的周长为![]() ,面积为
,面积为![]() ,可得2(a+b)=3,4ab=1,由(2)的结论可得
,可得2(a+b)=3,4ab=1,由(2)的结论可得![]() ,得到
,得到![]() ,进而求出
,进而求出![]() 的值即可.
的值即可.
(1)由操作可知,图1中每个小长方形的长为a,宽为b,
则图2中大正方形的边长为a+b,小正方形(阴影部分)的边长为a-b;
故答案为a+b,a-b;
(2)∵每个小长方形的长为a,宽为b,
∴每个小长方形的面积为ab,
∴(a+b)2-4ab=(a-b)2;
(3)设长方形长为2a,宽为2b,
∵长方形的周长为![]() ,面积为
,面积为![]() ,
,
∴2(a+b)=3,4ab=1,
∵(a-b)2=(a+b)2-4ab,
∴![]() ,
,
∴![]() 或
或![]() (不合题意,舍去).
(不合题意,舍去).
∴![]() ,
,
即该长方形长与宽的差为![]() .
.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分 | 人数/人 |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.

