题目内容
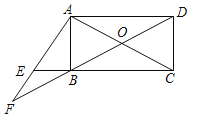
【题目】如图,在Rt△ABC中,AC=BC,AB=10,以AB为斜边向上作Rt△ABD,使∠ADB=90°.连接CD,若CD=7![]() ,则AD=_____.
,则AD=_____.
【答案】6或8
【解析】
首先证明A,C,B,D四点共圆,再根据AC=BC,即可得出∠ADC=∠ABC=45°,作AE⊥CD于E,则△AED是等腰直角三角形,设AE=DE=x,则AD=![]() x,在直角三角形ACE中,根据勾股定理即可求得.
x,在直角三角形ACE中,根据勾股定理即可求得.
如图,∵∠ACB=∠ADB=90°,
∴A,C,B,D四点共圆,
又∵AC=BC,
∴∠BAC=∠ABC=45°,
∴∠ADC=∠ABC=45°,
作AE⊥CD于E,
∴△AED是等腰直角三角形,
设AE=DE=x,则AD=![]() x,
x,
∵CD=7![]() ,
,
∴CE=7![]() ﹣x,
﹣x,
∵AB=10,
∴AC=![]() AB=5
AB=5![]() ,
,
在Rt△AEC中,AC2=AE2+EC2,
∴(5![]() )2=x2+(7
)2=x2+(7![]() ﹣x)2
﹣x)2
解得x=4![]() 或3
或3![]() ,
,
∴AD=![]() x=8或6,
x=8或6,
故答案为6或8.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目