题目内容
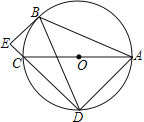
【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EBEC.
(1)求证:四边形ABCD是矩形;
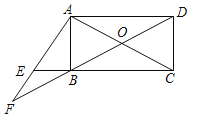
(2)延长DB、AE交于点F,若AF=AC,求证:AE=BF.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据AE2=EBEC证明△AEB∽△CEA,即可得到∠EBA=∠EAC=90°,从而说明平行四边形ABCD是矩形;
(2)根据(1)中△AEB∽△CEA可得![]() ,再证明△EBF∽△BAF可得
,再证明△EBF∽△BAF可得![]() ,结合条件AF=AC,即可证AE=BF.
,结合条件AF=AC,即可证AE=BF.
证明:(1)∵AE2=EBEC
∴![]()
又∵∠AEB=∠CEA
∴△AEB∽△CEA
∴∠EBA=∠EAC
而∠EAC=90°
∴∠EBA=∠EAC=90°
又∵∠EBA+∠CBA=180°
∴∠CBA=90°
而四边形ABCD是平行四边形
∴四边形ABCD是矩形
即得证.
(2)∵△AEB∽△CEA
∴![]() 即
即![]() ,∠EAB=∠ECA
,∠EAB=∠ECA
∵四边形ABCD是矩形
∴OB=OC
∴∠OBC=∠ECA
∴∠EBF=∠OBC=∠ECA=∠EAB
即∠EBF=∠EAB
又∵∠F=∠F
∴△EBF∽△BAF
∴![]()
∴![]()
而AF=AC
∴BF=AE
即AE=BF得证.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目