题目内容
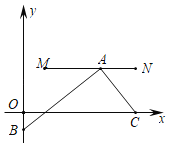
【题目】《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．其中第九卷《勾股》章，主要讲述了以测量问题为中心的直角三角形三边互求的关系．其中记载：“今有邑，东西七里，南北九里，各中开门，出东门一十五里有木，问：出南门几何步而见木？”
译文：“今有一座长方形小城，东西向城墙长7里，南北向城墙长9里，各城墙正中均开一城门．走出东门15里处有棵大树，问走出南门多少步恰好能望见这棵树？”（注：1里＝300步）
你的计算结果是：出南门几何步而见木（ ）
A.300步B.315步C.400步D.415步
【答案】B
【解析】
根据题意写出AB、AC、CD的长，根据相似三角形的性质得到比例式，计算即可．
解：由题意得，AB=15里，AC=4.5里，CD=3.5里，
∵AC⊥CD，AB⊥AC，DE⊥CD，
∴CD∥AB，AC∥DE，
∴∠DEC=∠ACB，∠DCE=∠ABC，
∴△ACB∽△DEC，
∴
，即
，
解得，DE=1.05里=315步，
∴走出南门315步恰好能望见这棵树．
故选：B．
一本好题口算题卡系列答案
【题目】包河区发展农业经济产业，在大圩乡种植多品种的葡萄.已知某葡萄种植户李大爷的葡萄成本为10元
，如果在未来40天葡萄的销售单价
（元）与时间
（天）之间的函数关系式为：
，且葡萄的日销售量
（千克）与时间（天）的关系如下表：
时间 | 1 | 3 | 6 | 10 | 20 | 40 |
日销售量 | 118 | 114 | 108 | 100 | 80 | 40 |
（1）请直接写出与之间的变化规律符合什么函数关系？并求在第15天的日销售量是多少千克？
（2）在后20天（即
），请求出哪一天的日销售利润最大？日销售利润最大为多少？
（3）在实际销售的前20天中，李大爷决定每销售1千克水果就捐赠
元利润（
）给留守贫困儿童作为助学金，前20天销售完后李大爷发现，每天扣除捐赠后的日销售利润随时间
的增大而增大，请求出的取值范围.
