题目内容
【题目】(1)如图(1),将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图(2)形状拼成一个正方形.
①图(2)中的空白部分的边长是多少?(用含a,b的式子表示)
②观察图(2),用等式表示出![]() ,ab和
,ab和![]() 的数量关系;
的数量关系;

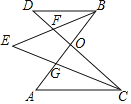
(2)如图所示,在△ABC与△DCB中,AC与BD相交于点E,且∠A=∠D,AB=DC.求证:△ABE≌△DCE;

【答案】(1)①2a-b;②![]() =
=![]() -8ab;(2)见解析
-8ab;(2)见解析
【解析】
(1)①先计算空白正方形的面积,再求边长;
②利用等量关系式S空白=S大正方形-4个S长方形代入即可;
(2)分析题意,根据∠A=∠D,AB=DC以及对顶角就可证明两三角形全等.
(1)①∵图(2)中的空白部分的面积=![]() -4a×2b=4
-4a×2b=4![]() +4ab+
+4ab+![]() -8ab=
-8ab=![]() ,
,
∴图(2)中的空白部分的边长是:2a-b;
②∵S空白=S大正方形-4个S长方形,
∴![]() =
=![]() -4×2a×b,
-4×2a×b,
则![]() =
=![]() -8ab;
-8ab;
(2) 证明: ∵在△ABE和△DCE中,
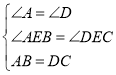
∴△ABE≌△DCE;

练习册系列答案
相关题目
【题目】安庆市在精准扶贫活动中,因地制宜指导农民调整种植结构,增加种植效益,2018年李大伯家在工作队的帮助下,计划种植马铃薯和蔬菜共15亩,预计每亩的投入与产出如下表:(每亩产出-每亩投入=每亩纯收入)
种类 | 投入(元) | 产出(元) |
马铃薯 | 1000 | 4500 |
蔬菜 | 1200 | 5300 |
(1)如果这15亩地的纯收入要达到54900元,需种植马铃薯和蔬菜各多少亩?
(2)如果总投入不超过16000元,则最多种植蔬菜多少亩?该情况下15亩地的纯收入是多少?