题目内容
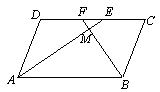
如图,O为矩形ABCD的中心,将直角三角板的直角顶点与O点重合,转动三角板使两直角边始终与BC,AB相交,交点分别为M,N.如果AB=4,AD=6,OM=x,ON=y.则y与x的关系是( )
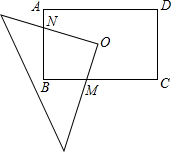

A. | B. | C.y=x | D. |
D
作OF⊥BC,OE⊥AB,则有∠OEN=∠OFM=90°.
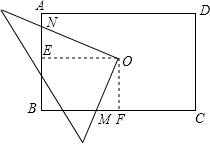
∵∠EOF=90°,
∴∠MOF=∠EOF-∠EOM=90°-∠EOM,
∵∠NOE=∠NOM-∠EOM=90°-∠EOM,
∴∠MOF=∠NOE,
∴△OEN与△OFM相似.
∴OE:OF=ON:OM,
∴ ,∴
,∴ 故选D.
故选D.

∵∠EOF=90°,
∴∠MOF=∠EOF-∠EOM=90°-∠EOM,
∵∠NOE=∠NOM-∠EOM=90°-∠EOM,
∴∠MOF=∠NOE,
∴△OEN与△OFM相似.
∴OE:OF=ON:OM,
∴
 ,∴
,∴ 故选D.
故选D.
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
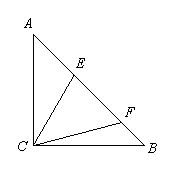
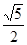 ,DE=2,求AD的长.
,DE=2,求AD的长.
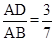 ,则EC的长是( )
,则EC的长是( )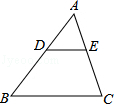
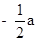 B.
B.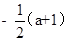 C.
C.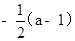 D.
D.