Question

【题目】如图，AC是⊙O的直径，PA切⊙O于点A，PB切⊙O于点B，且∠APB＝60°．

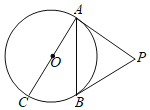
（1）求∠BAC的度数；

（2）若PA＝，求点O到弦AB的距离．

Answer 1

【答案】（1）30°；（2）2

【解析】

（1）根据切线长定理及切线的性质可得PA=PB，∠OAP=90°，由∠PAB=60°可证明△ABP是等边三角形，可得∠BAP=60°，即可求出∠BAC的度数；

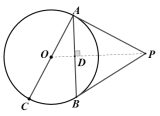
（2）连接OP，交AB于点D，根据切线长定理可得∠APO＝∠BPO=30°，即可得OP⊥AB，根据垂径定理可求出AD的长，根据含30°角的直角三角形的性质可得OA=2OD，利用勾股定理列方程求出OD的长即可得答案.

（1）∵PA，PB分别是⊙O的切线

∴PA=PB，∠OAP＝90°，

∵∠APB＝60°

∴△ABP为等边三角形

∴∠BAP＝60°

∴∠BAC＝90°﹣60°＝30°

（2）连接OP，交AB于点D．

∵△ABP为等边三角形

∴BA=PB=PA=，

∵PA，PB分别是⊙O的切线，

∴∠APO＝∠BPO=30°，

∴OP⊥AB，

∴AD＝AB=，

∵∠ODA＝90°，∠BAC＝30°，

∴OA=2 OD，

∵，

∴，

解得：OD=2，即点O到弦AB的距离为2．