题目内容
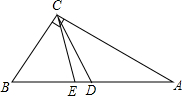已知：Rt△ABC中，∠C=90°，D点在AC边的垂直平分线上，CE平分∠ACB，∠A=35°，则∠DCE为
- A.20°
- B.15°
- C.10°
- D.5°
C
分析：由D点在AC边的垂直平分线上，根据线段垂直平分线的性质，即可求得∠DCA的度数，又由Rt△ABC中，∠C=90°，CE平分∠ACB，即可求得∠ECA的度数，继而求得∠DCE的度数．
解答：∵D点在AC边的垂直平分线上，
∴AD=CD，
∴∠DCA=∠A=35°，
∵Rt△ABC中，∠ACB=90°，CE平分∠ACB，
∴∠ECA=
∠ACB=45°，
∴∠DCE=∠ECA-∠DCA=45°-35°=10°．
故选C．
点评：此题考查了线段垂直平分线的性质、角平分线的定义．此题比较简单，解题的关键是掌握垂直平分线上任意一点，到线段两端点的距离相等定理的应用．
分析：由D点在AC边的垂直平分线上，根据线段垂直平分线的性质，即可求得∠DCA的度数，又由Rt△ABC中，∠C=90°，CE平分∠ACB，即可求得∠ECA的度数，继而求得∠DCE的度数．
解答：∵D点在AC边的垂直平分线上，
∴AD=CD，
∴∠DCA=∠A=35°，
∵Rt△ABC中，∠ACB=90°，CE平分∠ACB，
∴∠ECA=
∠ACB=45°，∴∠DCE=∠ECA-∠DCA=45°-35°=10°．
故选C．
点评：此题考查了线段垂直平分线的性质、角平分线的定义．此题比较简单，解题的关键是掌握垂直平分线上任意一点，到线段两端点的距离相等定理的应用．
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
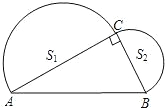如图，已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC、BC为直径作半圆，面积分别记为S1、S2，则S1+S2等于
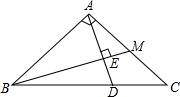如图，已知在Rt△ABC中，∠BAC=90°，AB=AC，M是AC的中点，AD⊥BM于E，交BC于D点．已知在Rt△ABC中，∠C=90°，sinA
，则tanB的值为（ ）
| ||
| 2 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
如图：已知在Rt△ABC中，∠C=90°，AC=4，BC=3，在直线AC上找点P，使△ABP是等腰三角形，则AP的长度为