题目内容
如图1,点A在x轴上,点D在y轴上,以OA、AD为边分别作等边△OAC和等边△ADE,若D(0,4),A(2,0).
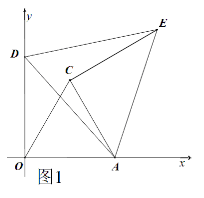
(1)若∠DAC=10°,求CE的长和∠AEC的度数.
(2)如图2,若点P为x轴正半轴上一动点,点P在点A的右边,连PC,以PC为边在第一象限作等边△PCM,延长MA交y轴于N,当点P运动时.
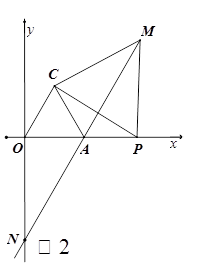
①∠ANO的值是否发生变化?若不变,求其值,若变化,请说明理由.
②AM-AP的值是否发生变化?若不变,求其值,若变化,请说明理由.

(1)若∠DAC=10°,求CE的长和∠AEC的度数.
(2)如图2,若点P为x轴正半轴上一动点,点P在点A的右边,连PC,以PC为边在第一象限作等边△PCM,延长MA交y轴于N,当点P运动时.

①∠ANO的值是否发生变化?若不变,求其值,若变化,请说明理由.
②AM-AP的值是否发生变化?若不变,求其值,若变化,请说明理由.
试题分析:(1)解答本题的关键是证明△DOA≌△ECA,由题意可由OA=CA、∠OAD=∠CAE、DA=EA判定△DOA≌△ECA,由此所求CE=DO,所求∠AEC=∠ADO.由∠DAC=10°、等边△COA可得∠OAD=50°,所以∠ADO=40°,所以∠AEC=40°.由点D的坐标为(0,4)可知:OD=4,所以CE=4.
①确定∠ANO的值是否发生变化,可想:在Rt△ONC中,∠OAN的度数是否发生变化.因为∠OAC=60°,
那么只要求出∠MAP或∠CAM的度数,此题就很容易求解了.可通过证明△OCP≌△ACM得出结论.
②在①中已得出△OCP≌△ACM,所以AM=OP,所以AM-AP=OP-AP=OA,可以看出无论点P如何运动,AM-AP的值始终等于OA.
试题解析:
解:(1)∵△OAC和△ADE是等边三角形
∴∠OAC=∠DAE=60°
∵∠DAC=10°
∴∠CAE=∠OAD=60○-∠CAD=50°
∵在△CAE 和△OAD中
AC=AO
∠CAE=∠OAD
AE=AD
∴△CAE ≌△DOA
∴CE=OD ∠AEC=∠ADO
∵点D的坐标是(0,4)
∴CE=OD=4
∴∠AEC=∠ADO=90°-50°=40°
(2)①.∠ANO=30°,理由如下:
∵∠OCA=∠MCP=60°
∴∠OCP=∠ACM,
∵在△OCP≌△ACM中
OC=CA
∠OCP=∠ACM,
CP=CM
∴△OCP≌△ACM
∴∠COA=∠CAM=60°
∴∠MAP=180°-120°=60°
∴∠OAN=∠MAP =60°
∴∠ANO=90O-60O=30O
②AM-AP=2,理由如下:
∵△OCP≌△ACM
∴AM=OP
∴AM-OP=OP-AP=OA
点A的坐标是(2,0)
∴OA=2
∴AM-AP=2

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目