Question

【题目】如图，已知抛物线y=x2+bx+c的顶点坐标为M（0，-1），与x轴交于A、B两点．

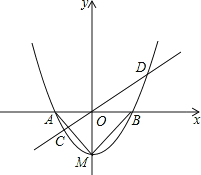
（1）求抛物线的解析式；

（2）判断△MAB的形状，并说明理由；

（3）过原点的任意直线（不与y轴重合）交抛物线于C、D两点，连接MC，MD，试判断MC、MD是否垂直，并说明理由．

Answer 1

【答案】（1）y=x2-1．（2）△MAB是等腰直角三角形．理由见解析；（3）MC⊥MD；理由见解析.

【解析】试题分析：（1）待定系数法即可解得．

（2）由抛物线的解析式可知OA=OB=OM=1，得出∠AMO=∠MAO=∠BMO=∠MBO=45°从而得出△MAB是等腰直角三角形．

（3）分别过C点，D点作y轴的平行线，交x轴于E、F，过M点作x轴的平行线交EC于G，交DF于H，设D（m，m2-1），C（n，n2-1），通过EG∥DH，得出，从而求得m、n的关系，根据m、n的关系，得出△CGM∽△MHD，利用对应角相等得出∠CMG+∠DMH=90°，即可求得结论．

试题解析：（1）∵抛物线y=x2+bx+c的顶点坐标为M（0，-1），

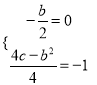∴，解得b=0，c=-1，

∴抛物线的解析式为：y=x2-1．

（2）△MAB是等腰直角三角形．

由抛物线的解析式为：y=x2-1可知A（-1，0），B（1，0），

∴OA=OB=OM=1，

∴∠AMO=∠MAO=∠BMO=∠MBO=45°，

∴∠AMB=∠AMO+∠BMO=90°，AM=BM，

∴△MAB是等腰直角三角形．

（3）MC⊥MD；

分别过C点，D点作y轴的平行线，交x轴于E、F，过M点作x轴的平行线交EC延长线于G，交DF于H，

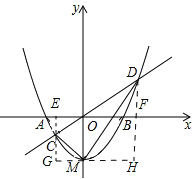
设D（m，m2-1），C（n，n2-1），

∴OE=-n，CE=1-n2，OF=m，DF=m2-1，

∵OM=1，

∴CG=n2，DH=m2，

∵EG∥DH，

∴，

即，

m（1-n2）=-n（m2-1），

m-mn2=-m2n+n，

（m2n-mn2）=-m+n，

mn（m-n）=-（m-n），

∴mn=-1

解得m=-，

∵， ，

∴，

∵∠CGM=∠MHD=90°，

∴△CGM∽△MHD，

∴∠CMG=∠MDH，

∵∠MDH+∠DMH=90°

∴∠CMG+∠DMH=90°，

∴∠CMD=90°，

即MC⊥MD．