题目内容
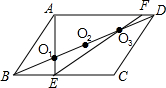（1997•河北）如图，已知在?ABCD中，O1、O2、O3为对角线BD上三点，且BO1=O1O2=O2O3=O3D，连接AO1并延长交BC于点E，连接EO3并延长交AD于点F，则AD：FD等于（ ）分析：先根据平行四边形的对边平行得出AD∥BC，再由平行线法证明出△BO3E∽△DO3F和△BO1E∽△DO1A，然后利用相似三角形的性质得出DF：BE的值及BE：AD的值，进而求出AD：DF的值．
解答：解：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴△BO3E∽△DO3F，△BO1E∽△DO1A，
∴BE：DF=BO3：DO3=3：1，BE：AD=BO1：DO1=1：3=3：9，
∴AD：DF=9：1．
故选B．
∴AD∥BC，
∴△BO3E∽△DO3F，△BO1E∽△DO1A，
∴BE：DF=BO3：DO3=3：1，BE：AD=BO1：DO1=1：3=3：9，
∴AD：DF=9：1．
故选B．
点评：本题考查了平行四边形的性质，相似三角形的判定与性质，根据相似三角形的性质列出比例式是解题的关键．
练习册系列答案
相关题目
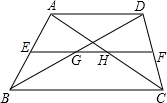（1997•河北）如图，在梯形ABCD中，AD∥BC，AD=12cm，BC=16cm，中位线EF与AC、BD分别相交于点H、G，则GH的长为
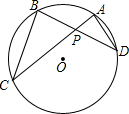（1997•河北）如图，已知⊙O的两条弦AC、BD相交于点P，∠ADB=25°，∠BPC=70°，则
点到达端点时，另一点也随之停止运动．设运动时间为t，求：