题目内容
【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AECF是正方形.直接写出答案,不需说明理由。
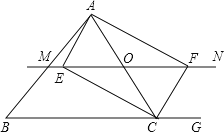
【答案】(1)OE=OF,理由详见解析;(2)当点O运动到AC的中点处,理由详见解析;(3)∠ACB=90°时.
【解析】试题分析:(1)利用角平分线的性质得出,∠1=∠2,进而得出,∠3=∠2,即可得出OE与OF的大小关系;
(2)首先证得四边形AECF是平行四边形,进而得出∠ECF=90°,再利用矩形的判定得出即可;
(3)由(2)证明可知,当点O运动到AC的中点时,四边形AECF是矩形,进而得出AC⊥MN,即可得出答案.
试题解析:(1)OE=OF,理由如下:
因为CE平分∠ACB,所以∠1=∠2,又因为MN∥BC,所以∠1=∠3,所以∠3=∠2,所以EO=CO,同理,FO=CO,所以OE=OF.
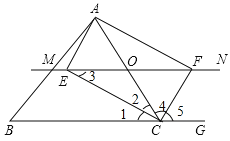
(2)当点O运动到AC的中点时,四边形AECF是矩形,理由如下:
因为OE=OF,点O是AC的中点,所以四边形AECF是平行四边形,又因为CF平分∠BCA的外角,所以∠4=∠5,又因为∠1=∠2,所以∠1=∠2,∠2+∠4=![]() =90°,即∠ECF=90°,所以平行四边形AECF是矩形.
=90°,即∠ECF=90°,所以平行四边形AECF是矩形.
(3)当△ABC是直角三角形时,即∠ACB=90°时,四边形AECF是正方形,理由如下:
由(2)证明可知,当点O运动到AC的中点时,四边形AECF是矩形,又因为∠ACB=90°,CE,CN分别是∠ACB与∠ACB的外角的平分线,所以∠1=∠2=∠3=∠4=∠5=45°,所以AC⊥MN,所以四边形AECF是正方形.

【题目】某校田径运动会上,参加男子跳高的16名运动员成绩如下表:
成绩(m) | 1.45 | 1.50 | 1.55 | 1.60 | 1.65 | 1.70 |
人数 | 3 | 4 | 3 | 2 | 3 | 1 |
则这些运动员成绩的中位数是( )
A. 1.5B. 1.55C. 1.60D. 1.65
