题目内容
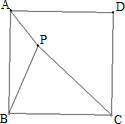 如图,P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP按顺时针方向旋转,使点A与点C重合,这时P点旋转到了G点.
如图,P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP按顺时针方向旋转,使点A与点C重合,这时P点旋转到了G点.
(1)请画出旋转后的图形,说出此时△APC绕点B旋转了多少度?
(2)求出PG的长度(可以不化简).
(3)请你猜想△PGC的形状,并说明理由.
(4)求∠APB的度数.
解:(1)旋转后的△BCG如图所示,
∵正方形ABCD,
∴对应边AB与BC的夹角∠ABC=90°,
则旋转角为90°;
(2)连接PG,由旋转的性质可知BP=BG,∠PBG=∠ABC=90°,
∴△BPG为等腰直角三角形,
又BP=BG=2,
∴PG=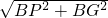 =2
=2 ;
;
(3)△PGC为直角三角形,理由如下:
证明:由旋转的性质可知CG=AP=1,已知PC=3,
由(2)可知PG=2 ,
,
∵PG2+CG2=(2 )2+12=9,PC2=9,
)2+12=9,PC2=9,
∴PG2+CG2=PC2,
∴△PGC为直角三角形;
(4)由旋转可知∠APB=∠BGC,
由(2)得到△BPG为等腰直角三角形,所以∠PGB=45°,
由(3)得到△PGC为直角三角形,所以∠PGC=90°,
则∠APB=∠BGC=∠PGB+∠PGC=90°+45°=135°.
分析:(1)根据正方形的性质得到∠ABC=90°,将△ABP沿顺时针方向旋转,使点A与点C重合时,旋转角为90°;
(2)连接PG,证明△BPG为等腰直角三角形,BP=BG=2,由勾股定理可求PG;
(3)猜想△PGC为直角三角形,理由:由旋转的性质可知CG=AP=1,已知PC=3,由(2)可知PG,利用勾股定理的逆定理,判断△PGC为直角三角形;
(4)由(3)得到∠PGC为直角,又(2)得到△BPG为等腰直角三角形,即可求出∠BGC的度数,由旋转可知∠APB等于∠BGC,即可得到∠APB的度数.
点评:本题考查了旋转的性质,正方形的性质,勾股定理及其逆定理的运用.解本题的关键是由旋转角为90°,对应边相等,得出等腰直角三角形.
∵正方形ABCD,
∴对应边AB与BC的夹角∠ABC=90°,
则旋转角为90°;

(2)连接PG,由旋转的性质可知BP=BG,∠PBG=∠ABC=90°,
∴△BPG为等腰直角三角形,
又BP=BG=2,
∴PG=
 =2
=2 ;
;(3)△PGC为直角三角形,理由如下:
证明:由旋转的性质可知CG=AP=1,已知PC=3,
由(2)可知PG=2
 ,
,∵PG2+CG2=(2
 )2+12=9,PC2=9,
)2+12=9,PC2=9,∴PG2+CG2=PC2,
∴△PGC为直角三角形;
(4)由旋转可知∠APB=∠BGC,
由(2)得到△BPG为等腰直角三角形,所以∠PGB=45°,
由(3)得到△PGC为直角三角形,所以∠PGC=90°,
则∠APB=∠BGC=∠PGB+∠PGC=90°+45°=135°.
分析:(1)根据正方形的性质得到∠ABC=90°,将△ABP沿顺时针方向旋转,使点A与点C重合时,旋转角为90°;
(2)连接PG,证明△BPG为等腰直角三角形,BP=BG=2,由勾股定理可求PG;
(3)猜想△PGC为直角三角形,理由:由旋转的性质可知CG=AP=1,已知PC=3,由(2)可知PG,利用勾股定理的逆定理,判断△PGC为直角三角形;
(4)由(3)得到∠PGC为直角,又(2)得到△BPG为等腰直角三角形,即可求出∠BGC的度数,由旋转可知∠APB等于∠BGC,即可得到∠APB的度数.
点评:本题考查了旋转的性质,正方形的性质,勾股定理及其逆定理的运用.解本题的关键是由旋转角为90°,对应边相等,得出等腰直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,若正方形ABCD周长为a,则EF+EG等于( )
如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,若正方形ABCD周长为a,则EF+EG等于( )A、
| ||
B、
| ||
| C、a | ||
| D、2a |
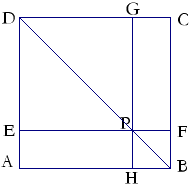 22、如图,ABCD是正方形,P是对角线BD上一点,过P点作直线EF、GH分别平行于AB、BC,交两组对边于E、F、G、H,则四边形PEDG,四边形PHBF都是正方形,四边形PEAH、四边形PGCF都是矩形,设正方形PEDG的边长是a,正方形PHBF的边长是b. 请动手实践并得出结论:
22、如图,ABCD是正方形,P是对角线BD上一点,过P点作直线EF、GH分别平行于AB、BC,交两组对边于E、F、G、H,则四边形PEDG,四边形PHBF都是正方形,四边形PEAH、四边形PGCF都是矩形,设正方形PEDG的边长是a,正方形PHBF的边长是b. 请动手实践并得出结论: ,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.
,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围. 点P,连接OP,OQ;
点P,连接OP,OQ;