题目内容
【题目】如图,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中不正确的是( ) 
A.∠DAE=∠CBE
B.△DEA不全等于△CEB
C.CE=DE
D.△EAB是等腰三角形
【答案】B
【解析】解:∵∠1+∠C+∠ABC=∠2+∠D+∠DAB=180°,且∠1=∠2,∠C=∠D, ∴∠ABC=∠DAB,
∴∠ABC﹣∠2=∠DAB﹣∠1,
∴∠DAB=∠CBA.故A正确;
在△DEA和△CEB中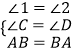 ,
,
∴△DEA≌△CEB(AAS),故B错误;
∴AC=BD.
∵∠1=∠2,
∴BE=AE,
∴△EAB是等腰三角形,AC﹣AE=BD﹣BE,故D正确;
∴CE=DE.故C正确.
故选B.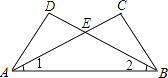
根据三角形的内角和定理就可以求出∠DAB=∠CBA,由等式的性质就可以得出∠DAE=∠CBE,根据AAS就可以得出△DEA≌△CEB;由△DEA≌△CEB就可以得出CE=DE,∠1=∠2就可以得出AE=BE,就可以得出结论.

练习册系列答案
相关题目