题目内容
【题目】如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.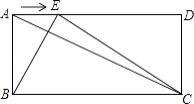
(1)若a=5,sin∠ACB= ![]() ,求b.
,求b.
(2)若a=5,b=10当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
【答案】
(1)解:∵四边形ABCD是矩形,
∴∠ABC=90°,
∵AB=a=5,sin∠ACB= ![]() ,
,
∴ ![]() ,
,
∴AC=13,
∴BC= ![]() =12,
=12,
∴b=12
(2)解:如图1,
∵BE⊥AC,
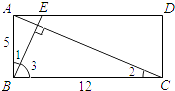
∴∠2+∠3=90°,
又∠1+∠3=90°,
∴∠1=∠2,
又∠BAE=∠ABC=90°,
∴△AEB∽△BAC,
∴ ![]() ,
,
即 ![]() ,
,
∴ ![]()
(3)解:∵点E在线段AD上的任一点,且不与A、D重合,
∴当△ABE与△BCE相似时,则∠BEC=90°
所以当△BAE∽△CEB(如图2)
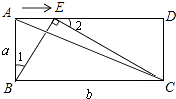
则∠1=∠BCE,
又BC∥AD,
∴∠2=∠BCE,
∴∠1=∠2, 。
又∠BAE=∠EDC=90°,
∴△BAE∽△EDC,
∴ ![]() ,
,
即 ![]() ,
,
∴x2﹣bx+a2=0,
即
![]() ,
,
当b2﹣4a2≥0,
∵a>0,b>0,
∴b≥2a,
即b≥2a时, ![]() ,
,
综上所述:当a、b满足条件b=2a时△BAE∽△CEB,此时 ![]() (或x=a);
(或x=a);
当a、b满足条件b>2a时△BAE∽△CEB,此时 ![]()
【解析】(1)根据矩形的性质得出∠ABC=90°,根据正弦三角函数得出AC,然后利用勾股定理得出BC的长,从而得出答案;
(2)根据同角的余角相等得出∠1=∠2,又∠BAE=∠ABC=90°,从而判断出△AEB∽△BAC,根据相似三角形对应边成比例得出答案;
(3)点E在线段AD上的任一点,且不与A、D重合,当△ABE与△BCE相似时,则∠BEC=90°,所以当△BAE∽△CEB(如图2),根据相似三角形的性质得出∠1=∠BCE,根据平行线的性质得出∠2=∠BCE,由等量代换得出∠1=∠2,又∠BAE=∠EDC=90°,从而判断出△BAE∽△EDC,根据相似三角形对应边成比例得出方程x2﹣bx+a2=0,将方程变形( x ![]() ) 2 =
) 2 =![]() ,当b2﹣4a2≥0,a>0,b>0,故b≥2a,综上所述得出结论
,当b2﹣4a2≥0,a>0,b>0,故b≥2a,综上所述得出结论
【考点精析】关于本题考查的矩形的性质和相似三角形的判定与性质,需要了解矩形的四个角都是直角,矩形的对角线相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】温州享有“中国笔都”之称,其产品畅销全球,某制笔企业欲将n件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示.设安排x件产品运往A地. 
(1)当n=200时,①根据信息填表:
A地 | B地 | C地 | 合计 | |
产品件数(件) | x | 2x | 200 | |
运费(元) | 30x |
②若运往B地的件数不多于运往C地的件数,总运费不超过4000元,则有哪几种运输方案?
(2)若总运费为5800元,求n的最小值.