Question

【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为56和32,则△EDF的面积为（）

A.10B.11C.12D.不能确定

Answer 1

【答案】C

【解析】

过点D作DH⊥AC于H，根据角平分线上的性质定理可得DF=DH，然后利用“HL”证明Rt△DEF和Rt△DGH全等，根据全等三角形的面积相等可得S△EDF=S△GDH，设面积为S，然后根据S△ADF=S△ADH列出方程求解即可．

如图，过点D作DH⊥AC于H，

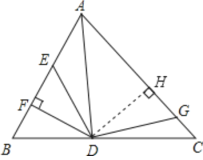
∵AD是△ABC的角平分线，DF⊥AB，

∴DF=DH，

在Rt△DEF和Rt△DGH中,

∴Rt△DEF≌Rt△DGH(HL)，

∴S△EDF=S△GDH，设面积为S，

在Rt△ADF和Rt△ADH中，

Rt△ADF≌Rt△ADH（HL），

∴S△ADF=S△ADH，

即32+S=56S，

解得S=12.

故选C.