题目内容
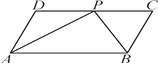
【题目】已知:如图所示,△ABC中,∠ABC=45°,高AE与高BD交于点M,BE=4,EM=3.
(1)△BEM与△AEC全等吗?请说明理由;
(2)BM与AC相等吗?请说明理由;
(3)求△ABC的面积.

【答案】(1)全等,理由见解析;(2)相等,理由见解析;(3)S△ABC=14.
【解析】
(1)根据已知条件易证AE=BE,再由AAS即可证明△BEM≌△AEC;(2)根据全等三角形的性质即可得BM=AC;(3)由(1)可知△BEM≌△AEC,根据全等三角形的性质可得BE=AE,EM=EC,再由三角形的面积公式计算即可.
(1)全等,
∵AE、BD为△ABC的高,
∴∠BEM=∠AEC=∠BDC=90°,
∴∠EBM+∠C=∠EBM+∠BME=90°,
∴∠BME=∠C,
又∠ABC=45°,
∴∠ABC=∠BAE=45°,
∴AE=BE,
在△BEM和△AEC中
∵
∴△BEM≌△AEC(AAS),
(2)相等,
∵△BEM≌△AEC,
∴BM=AC.
(3)∵△BEM≌△AEC,
∴BE=AE=4,EM=EC=3,
∴BC=BE+EC=7,
∴S△ABC=![]() ×7×4=14.
×7×4=14.

 名校课堂系列答案
名校课堂系列答案【题目】下面是淄博市2016年4月份的天气情况统计表:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 多云 | 阴 | 多云 | 晴 | 多云 | 阴 | 晴 | 晴 | 晴 | 多云 | 多云 | 多云 | 晴 | 晴 | 雨 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 雨 | 多云 | 多云 | 多云 | 多云 | 晴 | 多云 | 多云 | 晴 | 多云 | 多云 | 多云 | 晴 | 晴 | 晴 |
(1)请完成下面的汇总表:
天气 | 晴 | 多云 | 阴 | 雨 |
天数 |
(2)根据汇总表绘制条形图;
(3)在该月中任取一天,计算该天多云的概率.
【题目】某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
售价x(元/双) | 150 | 200 | 250 | 300 |
销售量y(双) | 40 | 30 | 24 | 20 |
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?