题目内容
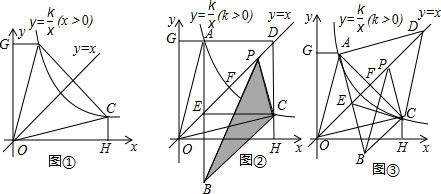
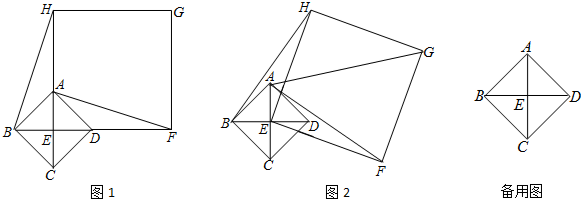
如图①,已知四边形ABCD是正方形,点E是AB的中点,点F在边CB的延长线上,且BE=BF,连接EF.
(1)若取AE的中点P,求证:BP= CF;
CF;
(2)在图①中,若将△BEF绕点B顺时针方向旋转α(0°<α<360°),如图②,是否存在某位置,使得AE∥BF?,若存在,求出所有可能的旋转角α的大小;若不存在,请说明理由;
(3)在图①中,若将△BEF绕点B顺时针旋转α(0°<α<90°),如图③,取AE的中点P,连接BP、CF,求证:BP= CF且BP⊥CF.
CF且BP⊥CF.

(1)证明:∵四边形ABCD是正方形,
∴BC=AB,
∵E为AB中点,P为AE中点,
∴2BE=2AE=AB,2PE=AE,
∵BE=BF,
∴CF=BC+BF=3BE,BP=BE+ BE=
BE= BE,
BE,
∴BP= CF.
CF.
(2)解:存在,
∵AE∥BF,
∵EB⊥BF,
∴EB⊥AE,
∴α=∠ABE,
∵cosα=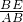 =
= ,
,
∴α=60°或300°.
存在,使得AE∥BF,当α=60°或300°时,AE∥BF.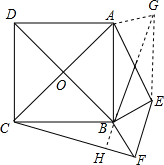
(3)证明:延长BP到G,使BP=PG,连接AG、EG,延长PB交CF于H,
∵AP=EP,BP=PG,
∴四边形ABEG是平行四边形,
∴AG=BE=BF,AG∥BE,
∴∠GAB+∠ABE=180°,
∵∠ABC=∠EBF=90°,
∴∠CBF+∠ABE=360°-180°=180°,
∴∠CBF=∠BAG,
在△AGB和△BCF中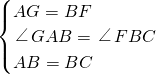 ,
,
∴△AGB≌△BCF,
∴CF=BG=2BP,∠ABG=∠BCF,
∴∠ABG+∠CBH=180°-90°=90°,
∴∠BCF+∠CBH=90°,
∴∠CHB=180°-90°=90°,
∴BP⊥CF,BP= CF.
CF.
分析:(1)根据正方形性质得出BC=AB,根据中点定义得出2BE=2AE=AB,2PE=AE,得出BE=BF,代入求出即可;
(2)根据平行线性质得出△AEB是直角三角形,根据cotα=
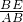 =
= ,求出α即可;
,求出α即可;(3)延长BP到G,使BP=PG,连接AG、EG,延长PB交CF于H,得出四边形ABEG是平行四边形,推出AG=BE=BF,AG∥BE,求出∠CBF=∠BAG,根据SAS证△AGB≌△BCF,推出CF=BG=2BP,∠ABG=∠BCF,求出∠CHB的度数即可.
点评:本题综合考查了正方形性质,全等三角形的性质和判定,平行线的性质,三角形的内角和定理,旋转性质,垂直定义等知识点的运用,本题的综合性比较强,培养了学生综合运用性质进行推理的能力,题目较好,但是有一定的难度,对学生提出较高的要求.

练习册系列答案
相关题目