题目内容
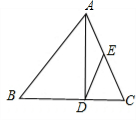 已知:如图,在△ABC中,AD是边BC上得高,E为边AC得中点,BC=14,AD=12,sinB=
已知:如图,在△ABC中,AD是边BC上得高,E为边AC得中点,BC=14,AD=12,sinB=| 4 | 5 |
求:(1)线段DC的长;
(2)tan∠EDC的值;
(3)求sin∠BAC.
分析:(1)根据sinB=
,先求出AB的长,然后求得BD,从而得出线段DC的长;
(2)先判断∠EDC=∠ECD,在Rt△ACD中,再求tan∠ECD的值,即tan∠EDC的值;
(3)根据三角形的面积,求出AB边上的高,从而求得sin∠BAC.
| 4 |
| 5 |
(2)先判断∠EDC=∠ECD,在Rt△ACD中,再求tan∠ECD的值,即tan∠EDC的值;
(3)根据三角形的面积,求出AB边上的高,从而求得sin∠BAC.
解答: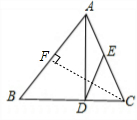 解:(1)∵sinB=
解:(1)∵sinB=
,
∴
=
,
∵AD=12,
∴AB=15,
由勾股定理得,BD=
=
=9,
∵BC=14,
∴线段DC的长=14-9=5;
(2)∵E为边AC的中点,AD是边BC上的高,
∴AE=EC=DE,(直角三角形斜边上的中线等于斜边的一半)
∴DE=EC,
∴∠EDC=∠ECD,
∴tan∠EDC=tan∠ECD=
=
;
(3)过点C作CF⊥AB,
∵S△ABC=BC•AD÷2=14×12÷2=84,
∴AB•CF÷2=84,
∴CF=
,
∴sin∠BAC=
=
×
=
.
 解:(1)∵sinB=
解:(1)∵sinB=| 4 |
| 5 |
∴
| AD |
| AB |
| 4 |
| 5 |
∵AD=12,
∴AB=15,
由勾股定理得,BD=
| AB2-AD2 |
| 152-122 |
∵BC=14,
∴线段DC的长=14-9=5;
(2)∵E为边AC的中点,AD是边BC上的高,
∴AE=EC=DE,(直角三角形斜边上的中线等于斜边的一半)
∴DE=EC,
∴∠EDC=∠ECD,
∴tan∠EDC=tan∠ECD=
| AD |
| CD |
| 12 |
| 5 |
(3)过点C作CF⊥AB,
∵S△ABC=BC•AD÷2=14×12÷2=84,
∴AB•CF÷2=84,
∴CF=
| 56 |
| 5 |
∴sin∠BAC=
| CF |
| AC |
| 56 |
| 5 |
| 1 |
| 13 |
| 56 |
| 65 |
点评:本题考查了勾股定理、三角函数的定义以及三角形的面积.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2, (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D. 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E. 已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,