Question

【题目】如图，在△ABC中，AB=CB，∠BAC＝∠BCA＝45°，F为AB延长线上一点，点E在BC上，且BE=BF．∠CAE=30°，求∠ACF的度数．

Answer 1

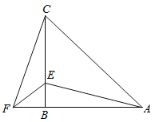
【答案】答案见解析.

【解析】

由∠BAC=∠BCA=45°，可得△ABC为等腰直角三角形，则可得到∠BAE=15°，再根据Rt△ABE≌Rt△CBF得到∠BCF=∠BAE=15°，然后根据∠ACF=∠BCF+∠BCA进行计算．

解：∵∠BAC＝∠BCA＝45°，

∴∠ABC=∠FBC=90°，

∴在Rt△ABE和Rt△CBF中

∴Rt△ABE≌Rt△CBF，

∵∠CAE=30°，
∴∠BAE=45°-30°=15°，

∵Rt△ABE≌Rt△CBF，
∴∠BCF=∠BAE=15°，
∴∠ACF=∠BCF+∠BCA=15°+45°=60°．