��Ŀ����
��ͼ����ƽ��ֱ������ϵ����һ����ABCO��OΪԭ�㣩����A��C�ֱ���x�ᡢy���ϣ���C������Ϊ(0��6)������BCD��BD�۵�(D����OC���ϣ���ʹC������DA�ߵ�E���ϣ�������BAE��BE�۵���ǡ��ʹ��A����BD�ߵ�F���ϣ�
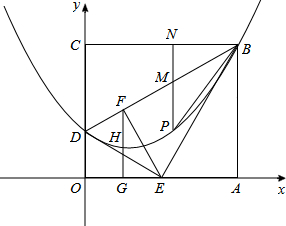
��1����BC�ij��������ۺ�BD����ֱ�ߵĺ�������ʽ��
��2������F��FG��x�ᣬ����ΪG��FG���е�ΪH����������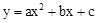 ����B,H, D���㣬�������߽���ʽ��
����B,H, D���㣬�������߽���ʽ��
��3����P�Ǿ����ڲ��ĵ㣬�ҵ�P�ڣ�2���е����������˶�������B, D�㣩������P��PN��BC���ֱ�BC �� BD�ڵ�N, M���Ƿ���������ĵ�P��ʹ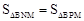 ������ڣ������P�����ꣻ��������ڣ���˵�����ɣ�
������ڣ������P�����ꣻ��������ڣ���˵�����ɣ�

��1����BC�ij��������ۺ�BD����ֱ�ߵĺ�������ʽ��
��2������F��FG��x�ᣬ����ΪG��FG���е�ΪH����������
 ����B,H, D���㣬�������߽���ʽ��
����B,H, D���㣬�������߽���ʽ����3����P�Ǿ����ڲ��ĵ㣬�ҵ�P�ڣ�2���е����������˶�������B, D�㣩������P��PN��BC���ֱ�BC �� BD�ڵ�N, M���Ƿ���������ĵ�P��ʹ
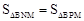 ������ڣ������P�����ꣻ��������ڣ���˵�����ɣ�
������ڣ������P�����ꣻ��������ڣ���˵�����ɣ��⣺��1���ɷ��ۿ�֪����BCD�ա�BED�����CBD=��DBE��
�֡ߡ�ABE�ա�FBE�����DBE=��ABE��
�֡��ı���OCBAΪ���Σ����CBD=��DBE=��ABE=30�㡣
��Rt��DOE�У���ODE=60�㣬��DE=CD=2OD��
��OC=OD+CD=6����OD+2OD=6����OD=2��D��0��2������CD=4��
��Rt��CDB�У�BC=CD•tan60��=4 ����B��4
����B��4 ��6����
��6����
��ֱ��BD�Ľ���ʽΪy=kx+b��������ã�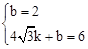 �����
�����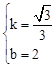 ��
��
��ֱ��BD�Ľ���ʽΪ��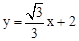 ��
��
��2����Rt��FGE�У���FEG=60�㣬FE=AE��
�ɣ�1���ã�OE=2 ����FE=AE=2
����FE=AE=2 ��
��
��FG=3��GE= ����OG=
����OG= ��
��
��H��FG���е㣬��H�� ��
��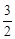 ����
����
��������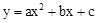 ����B��H��D���㣬
����B��H��D���㣬
��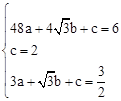 �����
�����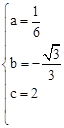 ��
��
�������߽���ʽΪ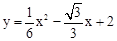 ��
��
��3�����ڡ�
��P���������ϣ�����P��x��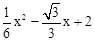 ����M��x��
����M��x��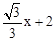 ����N��x��6����
����N��x��6����
��S��BNM=S��BPM����PM=MN������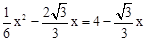 ��
��
�����ã�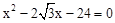 ����ã�x=2
����ã�x=2 ��x=4
��x=4 ��
��
��x=2 ʱ��
ʱ��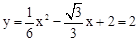 ��
��
��x=4 ʱ��
ʱ�� �����B�غϣ����������⣬��ȥ��
�����B�غϣ����������⣬��ȥ��
��P��2 ��2����
��2����
����ڵ�P��ʹS��BNM=S��BPM����P������Ϊ��2 ��2����
��2����
�֡ߡ�ABE�ա�FBE�����DBE=��ABE��
�֡��ı���OCBAΪ���Σ����CBD=��DBE=��ABE=30�㡣
��Rt��DOE�У���ODE=60�㣬��DE=CD=2OD��
��OC=OD+CD=6����OD+2OD=6����OD=2��D��0��2������CD=4��
��Rt��CDB�У�BC=CD•tan60��=4
 ����B��4
����B��4 ��6����
��6������ֱ��BD�Ľ���ʽΪy=kx+b��������ã�
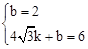 �����
�����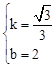 ��
����ֱ��BD�Ľ���ʽΪ��
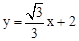 ��
����2����Rt��FGE�У���FEG=60�㣬FE=AE��
�ɣ�1���ã�OE=2
 ����FE=AE=2
����FE=AE=2 ��
����FG=3��GE=
 ����OG=
����OG= ��
����H��FG���е㣬��H��
 ��
��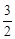 ����
������������
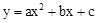 ����B��H��D���㣬
����B��H��D���㣬��
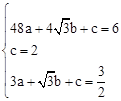 �����
�����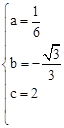 ��
���������߽���ʽΪ
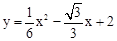 ��
����3�����ڡ�
��P���������ϣ�����P��x��
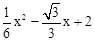 ����M��x��
����M��x��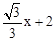 ����N��x��6����
����N��x��6������S��BNM=S��BPM����PM=MN������
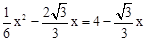 ��
�������ã�
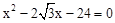 ����ã�x=2
����ã�x=2 ��x=4
��x=4 ��
����x=2
 ʱ��
ʱ��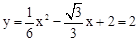 ��
����x=4
 ʱ��
ʱ�� �����B�غϣ����������⣬��ȥ��
�����B�غϣ����������⣬��ȥ����P��2
 ��2����
��2��������ڵ�P��ʹS��BNM=S��BPM����P������Ϊ��2
 ��2����
��2���������������1���������۵����ʵõ���CBD=��DBE=��ABE=30�㣬Ȼ���ֱ�������εõ���D����B�����꣬����ô���ϵ�������ֱ��BD�Ľ���ʽ��
��2����B��D�����Ѿ�������ؼ��������H�����꣮��Rt��FGE�У���ֱ�������������H�����꣬�����ô���ϵ������������ߵĽ���ʽ��
��3����S��BNM=S��BPM���������������εȸߣ����Եõ�PM=MN���ɴ˽��ۣ��г����������P�����ꡣ

��ϰ��ϵ�д�
�����Ŀ
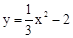 ����A��B���㣬��A����y����࣬P�������Ϊ��0����4��������PA��PB��������˵����
����A��B���㣬��A����y����࣬P�������Ϊ��0����4��������PA��PB��������˵����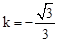 ʱ��BP2=BO•BA��
ʱ��BP2=BO•BA��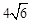 ��
��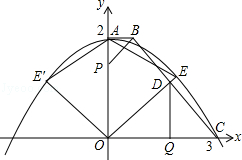
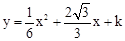 �ϣ���������߶�Ӧ�ĺ�������ʽ��
�ϣ���������߶�Ӧ�ĺ�������ʽ��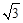 ����m��ֵ��
����m��ֵ��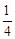 �����ʱBP�ij��ȣ�
�����ʱBP�ij��ȣ�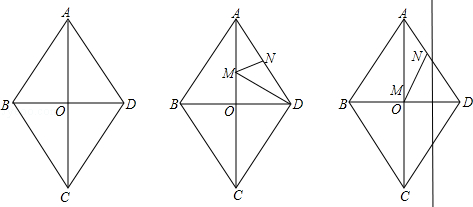
 ����A��B���㣮
����A��B���㣮
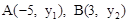 ����������
����������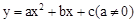 �ϣ���
�ϣ���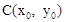 �Ǹ������ߵĶ��㣬��
�Ǹ������ߵĶ��㣬��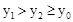 ����
����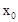 ��ȡֵ��Χ�ǡ� ��
��ȡֵ��Χ�ǡ� ��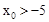
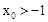
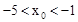
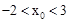
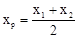 ��ͬ��
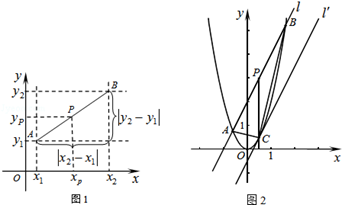
��ͬ��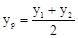 ������AB���е�����Ϊ
������AB���е�����Ϊ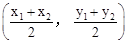 ���ɹ��ɶ�����
���ɹ��ɶ�����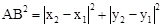 ������A��B�����ľ��빫ʽΪ
������A��B�����ľ��빫ʽΪ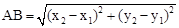 ��
��