题目内容
如图所示,某边防部接到情报,近海外有一可疑船只A正向公海方向行驶,边防部迅速派出快艇B追赶,在追赶过程中,设快艇B相对于海岸的距离为y1(海里),可疑船只A相对于海岸的距离为y2(海里),追赶时间为t(分钟),图中lA、lB分别表示y2、y1与t之间的关系,结合图象回答下列问题:

(1)请你根据图中标注的数据,分别求出y1、y2与t之间的函数关系式,并写出自变量的取值范围;
(2)15分钟内B能否追上A?说明理由;
(3)已知当A逃到离海岸12海里的公海时,B将无法对其进行检查,照此速度计算,B能否在A逃入公海前将其拦截?
答案:
解析:
解析:
|
(1)设lB:y1=kt+b,经过点(0,0)和(10,5)∴y1= (2)当t=15时,y1= (3)由 |

练习册系列答案
相关题目
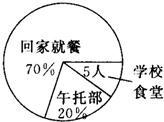 35、如图所示是某校六年级(1)班学生中午就餐情况统计图,问:
35、如图所示是某校六年级(1)班学生中午就餐情况统计图,问: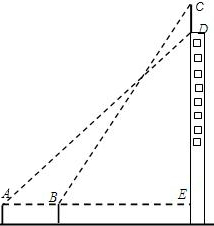 如图所示,某电视台大楼顶部安置了一电视发射铁塔CD,甲,乙两位调查员分别在楼下相距16米的A,B两处测得D点和C点的仰角分别是45°和60°,且A,B,E三点在一条直线上,若BE=30米,求这个电视发射铁塔的高度.(取
如图所示,某电视台大楼顶部安置了一电视发射铁塔CD,甲,乙两位调查员分别在楼下相距16米的A,B两处测得D点和C点的仰角分别是45°和60°,且A,B,E三点在一条直线上,若BE=30米,求这个电视发射铁塔的高度.(取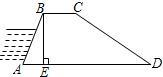 如图所示,某河堤的横断面是梯形ABCD,BC∥AD,迎水坡AB长13米,且tan∠BAE=
如图所示,某河堤的横断面是梯形ABCD,BC∥AD,迎水坡AB长13米,且tan∠BAE=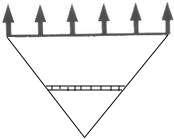 如图所示,某校宣传栏后面2米处种了一排树,每隔2米一棵,共种了6棵,小勇站在距宣传栏中间位置的垂直距离3米处,正好看到两端的树干,其余的4棵均被挡住,那么宣传栏的长为( )米.(不计宣传栏的厚度)
如图所示,某校宣传栏后面2米处种了一排树,每隔2米一棵,共种了6棵,小勇站在距宣传栏中间位置的垂直距离3米处,正好看到两端的树干,其余的4棵均被挡住,那么宣传栏的长为( )米.(不计宣传栏的厚度)