题目内容
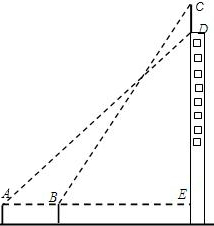 如图所示,某电视台大楼顶部安置了一电视发射铁塔CD,甲,乙两位调查员分别在楼下相距16米的A,B两处测得D点和C点的仰角分别是45°和60°,且A,B,E三点在一条直线上,若BE=30米,求这个电视发射铁塔的高度.(取
如图所示,某电视台大楼顶部安置了一电视发射铁塔CD,甲,乙两位调查员分别在楼下相距16米的A,B两处测得D点和C点的仰角分别是45°和60°,且A,B,E三点在一条直线上,若BE=30米,求这个电视发射铁塔的高度.(取| 3 |
分析:首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形△ADE、△CBE,应利用BE=AE-AB=30构造方程,进而可求出答案.
解答:解:设电视发射铁塔高x米.
Rt△ADE中,∠DAE=45°
∴AE=DE=16+30=46,CE=46+x;
Rt△CBE中,∠CBE=60°,tan∠CBE=
,
即:
=
;
解得:x=5.9≈6;
答:电视发射铁塔高6米.
Rt△ADE中,∠DAE=45°
∴AE=DE=16+30=46,CE=46+x;
Rt△CBE中,∠CBE=60°,tan∠CBE=
| CE |
| BE |
即:
| 3 |
| 46+x |
| 30 |
解得:x=5.9≈6;
答:电视发射铁塔高6米.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
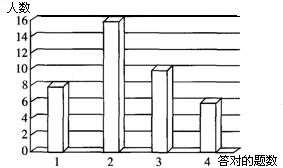
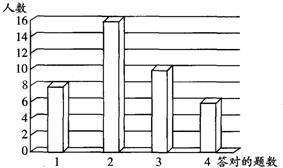 23、某电视台在一次青年歌手大赛中,设置了基础知识问答题,答对一题得5分,答错或不答得0分,各选手答对题的情况如图所示.
23、某电视台在一次青年歌手大赛中,设置了基础知识问答题,答对一题得5分,答错或不答得0分,各选手答对题的情况如图所示.