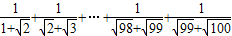题目内容
阅读理解并解题:例:解不等式:
| 3x+2 |
| x-1 |
解:把不等式
| 3x+2 |
| x-1 |
| 3x+2 |
| x-1 |
| x+4 |
| x-1 |
则有 (1)
|
|
解不等式(1)得:x>1,解不等式(2)得:x<-4.
所以原不等式的解集是:x<-4 或x>1.
请根据以上解不等式的思想方法解不等式:
| x |
| 3x+1 |
分析:先根据题意把不等式的右边化为0的形式,再得到关于x的不等式组,求出x的取值范围即可.
解答:解:移项得,
-1≤0,即
≤0,
则有(1)
,(2)
,
由(1)得,x≤-
;由(2)得,x>-
.
故原不等式的解集为:x≤-
或x>-
.
| x |
| 3x+1 |
| -2x-1 |
| 3x+1 |
则有(1)
|
|
由(1)得,x≤-
| 1 |
| 2 |
| 1 |
| 3 |
故原不等式的解集为:x≤-
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题考查的是解一元一次不等式组,根据所给的解一元一次不等式的方法得到关于x的不等式组是解答此题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ;
;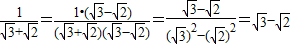
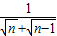 的结果吗?
的结果吗?
 ;
;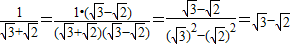
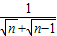 的结果吗?
的结果吗?