题目内容
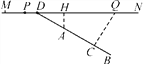
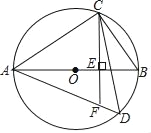
【题目】如图，AB是⊙O的直径，CE⊥AB于E，弦AD交CE延长线于点F，CF﹦AF．
（1）求证：
；
（2）若BC=8，tan∠DAC=
，求⊙O的半径．
【答案】（1）证明见解析；（2）8．
【解析】
（1）延长CF交⊙O于H，连接AH，根据垂径定理得到
，根据圆周角定理证明即可；
（2）根据直径所对的圆周角为90°，得到∠ACB=90°，根据圆周角定理得到∠B=∠DAC，根据正切的概念、勾股定理计算即可得出结论．
（1）延长CF交⊙O于H，连接AH．
∵CE⊥AB，∴．
∵CF=AF，∴∠FAC=∠FCA，∴
，∴
；
（2）∵AB是直径，∴∠ACB=90°．
∵，∴∠B=∠DAC，∴tanB
，即
，解得：AC=8
，∴AB
16，∴⊙O的半径为8．
练习册系列答案
学习实践园地系列答案
相关题目
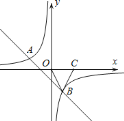
【题目】如图，一次函数
的图象与反比例函数
的图象交于
，
两点．
Ⅰ
试确定上述反比例函数和一次函数的表达式；
Ⅱ连OB，在x轴上取点C，使
，并求
的面积；
Ⅲ直接写出一次函数值大于反比例函数值的自变量x的取值范围．
