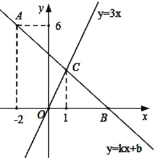
题目内容
【题目】如图,△ABC中,∠C=90°,⊙O是△ABC的内切圆,D、E、F是切点.
(1)求证:四边形ODCE是正方形;
(2)如果AC=6,BC=8,求内切圆⊙O的半径.
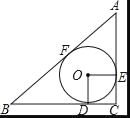
【答案】(1)证明见解析;(2)⊙O的半径为2.
【解析】
(1)根据三角形内切圆的性质可得OE⊥AC,OD⊥BC,OE=OD,据此可证明四边形ODCE是正方形;
(2)先根据勾股定理求出AB的长;接下来利用由切线长定理得,AF=AE,BD=BF,CD=CE,由CD+CE=BC+AC﹣BD﹣AE=BC+AC﹣AB即可求出⊙O的半径为2.
(1)∵⊙O是△ABC的内切圆,
∴OD⊥BC,OE⊥AC,又∠C=90°,
∴四边形ODCE是矩形,
∵OD=OE,
∴四边形ODCE是正方形;
(2)∵∠C=90°,AC=6,BC=8,
∴AB=![]() =10,
=10,
由切线长定理得,AF=AE,BD=BF,CD=CE,
∴CD+CE=BC+AC﹣BD﹣AE=BC+AC﹣AB=4,
则CE=2,即⊙O的半径为2.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目