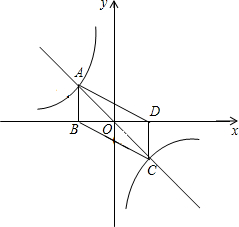
题目内容
如图,在同一个坐标系中,双曲线y=
与直线y=kx+b相交于A、B两点,点A的坐标为(2,1),另一个交点B的纵坐标为-4.
(1)求出这两个函数的解析式,并画出它们的图象;
(2)观察图象并回答:当x的取值在什么范围时,反比例函数值大于一次函数的值;
(3)当x取什么范围时,y=kx+b的值满足-2≤y<1.
(4)求△AOB的面积.
| k |
| x |
(1)求出这两个函数的解析式,并画出它们的图象;
(2)观察图象并回答:当x的取值在什么范围时,反比例函数值大于一次函数的值;
(3)当x取什么范围时,y=kx+b的值满足-2≤y<1.
(4)求△AOB的面积.

(1)∵把A(2,1)代入y=
得:k=2,
∴反比例函数的解析式是y=
;
把y=-4代入y=
得:-4=
,
x=-
,
∴B(-
,-4),
把A、B的坐标代入y=kx+b得:
,
解得:k=2,b=-3,
故一次函数的解析式是y=2x-3;
(2)如图: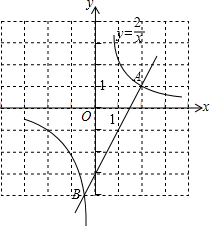
当x<-
或0<x<2时,反比例函数值大于一次函数的值;
(3)∵把y=-2代入y=2x-3得:x=
,
把y=1代入y=2x-3得:x=2,
当
≤y<2时,y=kx+b的值满足-2≤y<1.
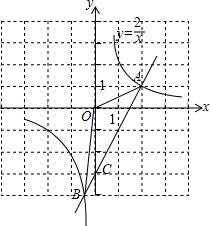
(4)∵把x=0代入y=2x-3得:y=-3,
∴OC=3,
∴△AOB的面积S=S△BOC+S△AOC=
×3×
+
×3×2=3
.
| k |
| x |
∴反比例函数的解析式是y=
| 2 |
| x |
把y=-4代入y=
| 2 |
| x |
| 2 |
| x |
x=-
| 1 |
| 2 |
∴B(-
| 1 |
| 2 |
把A、B的坐标代入y=kx+b得:
|
解得:k=2,b=-3,
故一次函数的解析式是y=2x-3;
(2)如图:

当x<-
| 1 |
| 2 |
(3)∵把y=-2代入y=2x-3得:x=
| 1 |
| 2 |
把y=1代入y=2x-3得:x=2,
当
| 1 |
| 2 |
(4)∵把x=0代入y=2x-3得:y=-3,
∴OC=3,
∴△AOB的面积S=S△BOC+S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |


练习册系列答案
相关题目